Table of Contents
गणितीय क्रिया (Mathematical Operations)
गणितीय क्रिया ही बुद्धिमत्ता चाचणी ची एक महत्त्वाची संकल्पना आहे जी सहसा विविध स्पर्धा परीक्षांमध्ये विचारली जाते. हा विषय उमेदवारांच्या विश्लेषणात्मक क्षमतेची चाचणी घेण्यासाठी विचारला जातो. हे दर्शविते की तुम्ही गोष्टींचे निरीक्षण करण्यात किती चांगले आहात. या विषयावर पूर्ण गुण मिळविण्यासाठी, तुम्ही पुरेशा प्रश्नांचा सराव केला पाहिजे आणि त्यामागील संकल्पना जाणून घ्या. येथे आम्ही तुम्हाला उदाहरणांसह गणिताचे प्रश्न सोडवण्याची पद्धत देत आहोत.
जिल्हा परिषद रिव्हिजन प्लॅन पाहण्यासाठी येथे क्लिक करा
जिल्हा परिषद परीक्षेचे वेळापत्रक 2023 पाहण्यासाठी येथे क्लिक करा
गणितीय क्रिया: विहंगावलोकन
खालील तक्त्यात आपण गणितीय क्रिया बद्दल विहंगावलोकन पाहू शकता.
| गणितीय क्रिया (Mathematical Operations): विहंगावलोकन | |
| श्रेणी | अभ्यास साहित्य |
| उपयोगिता | ZP भरती व सर्व स्पर्धा परीक्षांसाठी |
| विषय | बुद्धिमत्ता चाचणी |
| टॉपिकचे नाव | गणितीय क्रिया |
| महत्वाचे मुद्दे |
|
गणितीय क्रियांवर आधारित प्रश्न कसे सोडवायचे?
गणितीय क्रियांवर आधारित प्रश्नांचे प्रकार आहेत:
- दिलेली समीकरणे बरोबर आहेत की नाही
- चिन्हांच्या समतुल्य चिन्हांवर आधारित
- चिन्हांची अदलाबदल
- समीकरण संतुलित करणे
- समीकरण सोडवणे
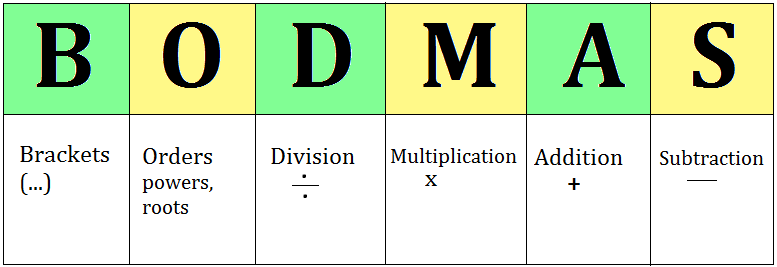
प्रत्येक प्रकारच्या गणितीय क्रियांवर आधारित प्रश्नासाठी, तुम्हाला फक्त एक नियम माहित असणे आवश्यक आहे तो म्हणजे BODMAS ज्याला आपण कं चे भा गु बे व म्हणतो.
B- Bracket (कंस) (), [], {}
O- (चे) Order, Square root, exponents, and powers
D- Division (भागाकार), ÷ /
M- Multiplication (गुणाकार) × *
A – Addition (बेरीज) +
S – Subtraction (वजाबाकी) –
याचा अर्थ तुम्ही कोणतेही समीकरण BODMAS क्रमाने सोडवले पाहिजे. प्रथम, कंस उघडा, नंतर घात, घातांक सोडवा, नंतर भागाकार करा आणि त्यानंतर गुणाकार, बेरीज आणि वजाबाकी करा.
(b) 8 ÷ 10 – 3 + 5 × 6 = 8
(c) 6 × 2 + 3 ÷ 12 – 3 = 15
(d) 3 ÷ 7 – 5 × 10 + 3 = 10
योग्य चिन्हे वापरून, आपल्याला मिळते:
(a) 15 × 5 + 5 – 20 ÷ 10 = 15 × 5 + 5 – 2 = 75 + 5 – 2 = 78
(c) 6 – 2 ÷ 3 + 12 × 3 = 6 – 2/3 + 36 = 42 – 2/3=124/3
(d) 3 + 7 × 5 – 10 ÷ 3 = 3 + 7 × 5 – 10/3=3+35-10/3=104/3 ∴ विधान (b) सत्य आहे
(a) 32
(b) 33
(c) 36
(d) यापैकी नाही
आपल्याकडे असलेली योग्य चिन्हे वापरून:
दिलेले समीकरण = 31 + 81 ÷ 9 – 7 = 31 + 9 – 7 = 33
(a) -1
(b) 2
(c) 0
(d) 1
योग्य चिन्हे वापरून, आपल्याकडे आहे:
दिलेले समीकरण = (4 × 15 + 12) ÷ 8 – 9 = 72 ÷ 8 – 9 = 9 – 9 = 0
Q4. जर Q चा अर्थ ‘जोडा’, J म्हणजे ‘गुणाकार’, T म्हणजे ‘वजाबाकी’ आणि K म्हणजे ‘भागाकार’, तर 26 K 2 Q 3 J 6 T 4 = ?
(a) 10
(b) 28
(c) 30
(d) 27
उत्तर.(d)
योग्य चिन्हे वापरून, आपल्याकडे आहे:
दिलेले समीकरण = 26 ÷ 2 + 3 × 6 – 4 = 13 + 18 – 4 = 27
Q5. जर ‘-‘ म्हणजे ‘भागा’, ‘+’ म्हणजे ‘गुणाकार’, ‘÷’ म्हणजे ‘वजाबाकी’ आणि ‘×’ म्हणजे ‘बेरीज’, तर खालीलपैकी कोणते समीकरण बरोबर आहे?
(a) 6 + 20 – 12 ÷ 7 – 1 = 38
(b) 6 – 20 ÷ 12 × 7 + 1 = 57
(c) 6 + 20 – 12 ÷ 7 × 1 = 62
(d) 6 ÷ 20 × 12 + 7 – 1 = 70
उत्तर.(d)
(d) मध्ये योग्य योग्य चिन्हे वापरून, आपल्याला विधान मिळते:
6 – 20 + 12 × 7 ÷ 1 = 6 – 20 + 84 = 90 – 20 = 70
Q6. जर L ने ÷, M ने ×, P ने + आणि Q ने – दर्शवितो, तर खालीलपैकी कोणते विधान सत्य आहे?
(a) 32 P 8 L 16 Q 4 =-2/3
(b) 6 M 18 Q 26 L 13 P 7 = 173/13
(c) 11 M 34 L 17 Q 8 L 3 =38/3
(d) 9 P 9 L 9 Q 9 M 9 = -71
उत्तर.(d)
(d) मध्ये योग्य चिन्हे वापरून, आपल्याला विधान मिळते:
9 + 9 ÷ 9 – 9 × 9 = 9 + 1 – 9 × 9 = 9 + 1 – 81 = 10 – 81 = -71.
Q7. चिन्हे आणि संख्यांमधील चार अदलाबदलांपैकी कोणते समीकरण योग्य बनवेल?
3 + 5 – 2 = 4
(a) + आणि –, 2 आणि 3
(b) + आणि –, 2 आणि 5
(c) + आणि –, 3 आणि 5
(d) यापैकी नाही
उत्तर.(c)
(a) मध्ये दिलेले अदलाबदल करून 2 – 5 + 3 = 4 or 0 = 4, जे चुकीचे आहे
(b) मध्ये दिलेले अदलाबदल करून 3 – 2 + 5 = 4 or 6 = 4, जे चुकीचे आहे
(c) मध्ये दिलेले अदलाबदल करून 5 – 3 + 2 = 4 or 4 = 4, जे बरोबर आहे
तर, उत्तर आहे (c).
Q8: या प्रश्नात, ∆ म्हणजे ‘पेक्षा जास्त आहे’, % म्हणजे ‘पेक्षा कमी आहे’, ⃞ म्हणजे ‘च्या बरोबर’, = म्हणजे ‘च्या बरोबरीचे नाही’, + म्हणजे ‘पेक्षा थोडे अधिक आहे. ‘, × म्हणजे ‘पेक्षा थोडे कमी आहे’. योग्य पर्याय निवडा.
Q8. जर a ∆ b आणि b + c असेल तर
(a) a % c
(b) c + a
(c) c % a
(d) म्हणू शकत नाही
उत्तर.(c)
a ∆ b ⇒ a > b आणि
b + c ⇒ b हा c पेक्षा थोडा जास्त आहे
⇒ a > c ⇒ c < a म्हणजे c % a
दिशानिर्देश (9-10): खालीलपैकी प्रत्येक प्रश्नामध्ये, अंकगणितीय क्रियांसाठी ग्रीक अक्षरे दिली आहेत. शीर्षस्थानी दिलेल्या दोन संबंधांवरून निश्चितपणे काढता येईल असे नाते शोधा.
ऑपरेशन्स: α ‘पेक्षा मोठा’ आहे, β ‘पेक्षा कमी’ आहे, γ ‘पेक्षा मोठा नाही’, δ ‘पेक्षा कमी नाही’, θ ‘च्या बरोबर’ आहे.
Q9. जर A α 2C आणि 2A θ 3B असेल तर
(a) C β B
(b) C δ B
(c) C α B
(d) C θ B
उत्तर.(a)
A α 2C ⇒ A > 2C
आणि 2A θ 3B ⇒ 2A = 3B
⇒ 2A > 4C आणि 2A = 3B
⇒ 3B > 4C ⇒ C < B म्हणजे C β B
Q10. जर B θ 2C आणि 3C γ A असेल तर
(a) B δ 2A
(b) B θ A
(c) 3B α 2A
(d) B β A
उत्तर.(d)
B θ 2C⇒ B = 2C
आणि 3C γ A ⇒ 3C ⊁ A
⇒B = 2C आणि 3C ≤ A
⇒ B = 2C < 3C ≤ A ⇒ B < A म्हणजे B β A

महाराष्ट्रातील सर्व स्पर्धा परीक्षांसाठी ऑनलाईन क्लास, व्हिडिओ कोर्स, टेस्ट सिरीज, पुस्तके आणि इतर अभ्यास साहित्य खाली दिलेल्या लिंक वर क्लिक करून मिळावा.
| ZP भरतीसाठी बुद्धिमत्ता चाचणी आणि अंकगणित | |
| बुद्धिमत्ता चाचणी | अंकगणित |
| अंकमालिका | |
| आरशातील आणि पाण्यातील प्रतिमा | अपूर्णांक व दशांश |
| अक्षरमालिका | शेकडेवारी |
| वेन आकृती | वेळ आणि काम |
| घनाकृती ठोकळे | नफा व तोटा |
| सांकेतिक भाषा | भागीदारी |
| दिशा व अंतर | सरासरी |
| रक्त संबंध (Blood Relation) | मसावी व लसावी |
| क्रम व स्थान (Order and Ranking) | वर्ग / घन व त्याचे मुळ |
| घड्याळ (Clock) | विभाज्यतेच्या कसोट्या |
| सरळव्याज सूत्र |
|
| ताज्या महाराष्ट्र सरकारी नोकरीबद्दल माहितीसाठी | माझी नोकरी 2023 |
| होम पेज | अड्डा 247 मराठी |
| मराठीत चालू घडामोडी | चालु घडामोडी |
अड्डा 247 मराठीचे युट्युब चॅनल
अड्डा 247 मराठी अँप | अड्डा 247 मराठी टेलिग्राम ग्रुप









