Table of Contents
Mensuration Formula For 2D And 3D Shapes
Mensuration Formula For 2D And 3D Shapes: Geometry is a branch of mathematics. One of the most important factors of Geometry is Mensuration. Mensuration is concerned with the measurement of different figures and geometric shapes. This includes the calculation of dimensions such as Perimeter, Area, Volume, Total Surface Area, etc. Mensuration is a very important factor in competitive exams. In this article, we will see the Mensuration Formula For 2D And 3D Shapes and some examples of Mensuration.
Mensuration Formula For 2D And 3D Shapes: Overview
This article provides you all necessary formule for 2D And 3D Shapes which is helpful for your upcoming Exams.
| Quantitative Aptitude Formulas: Formula | |
| Category | Study Material |
| Exam | All Competitive Exams |
| Subject | Geometry or Mensurations |
| Name | Mensuration Formula For 2D And 3D Shapes |
| Formula |
|
Mensuration Formula For 2D And 3D Shapes
Mensuration Formula For 2D And 3D Shapes: भूमिती ही गणिताची शाखा आहे. ज्यातील सर्वात महत्वाचा घटक म्हणजे मेन्सुरेशन (Mensuration). मेन्सुरेशन (Mensuration) हे वेगवेगळ्या आकृत्यांच्या मोजमापाशी आणि भूमितीच्या आकारांशी संबंधित आहे. यामध्ये आकारांची परिमिती (Perimeter), क्षेत्रफळ (Area), घनफळ (Volume), पृष्ठफळ (Total Surface Area) इत्यादींची गणना समाविष्ट आहे. स्पर्धा परीक्षेच्या अनुषंगाने मेन्सुरेशन फार महत्वाचा घटक आहे. सर्व स्पर्धा परीक्षेत यावर प्रश्न येतात. मेन्सुरेशन (Mensuration) वर पकड मिळवण्यासाठी आणि त्यावरील गणित सोडवण्यासाठी आपल्याला मेन्सुरेशन ची सूत्र (Mensuration Formula) माहिती असणे फार आवश्यक आहे. आज या लेखात आपण 2D आणि 3D आकारांसाठी मेन्सुरेशन फॉर्म्युला (Mensuration Formula For 2D And 3D Shapes) व त्यावरील काही उदाहरणे पाहणार आहे.
Mensuration Formula For 2D And 3D Shapes | 2D आणि 3D आकारांसाठी मेन्सुरेशन फॉर्म्युला
Mensuration Formula For 2D And 3D Shapes: मेन्सुरेशन चे सूत्र (Mensuration Formula) पाहतांना सर्वात आधी आपल्याला 2D आणि 3D आकार माहिती असणे आवश्यक आहे. खाली 2D आणि 3D आकार म्हणजे काय? याबद्दल सविस्तर माहिती खाली दिली आहे.
2D आकार– भूमितीमध्ये, एक द्विमितीय आकार म्हणजे एक सपाट आकृती किंवा एक आकार ज्यामध्ये फक्त दोन परिमाणे (dimensions) आहेत जसे की, लांबी (Length) आणि रुंदी (Width). द्विमितीय किंवा 2-D आकारांमध्ये कोणतीही जाडी (Thickness) नसते आणि ते फक्त दोन परिमाणांमध्ये मोजता येते. 2D आकारांचे केवळ क्षेत्रफळ (Area) आणि परिमिती (Perimeter) मोजली जाऊ शकते.
3D आकार– एक त्रिमितीय आकार आहे जिथे आकृतीचे तीन परिमाण आहेत. 3D आकाराला लांबी (Length), रुंदी (Width) आणि जाडी (Thickness) किवा उंची (Height) असते. या आकारांचे, क्षेत्रफळ (Area), घनफळ (Volume), पृष्ठफळ (Total Surface Area), वक्र पृष्ठभागाचे क्षेत्रफळ (Curved Surface Area) काढता येते.

Quantitative Aptitude Formulas
Mensuration Formula For 2D Shapes | 2D आकारांसाठी मेन्सुरेशन फॉर्म्युला
Mensuration Formula For 2D Shapes: 2D आकारांपैकी काहींचे क्षेत्रफळ (Area) आणि परिमितीचे (Perimeter) सूत्र खालील तक्त्यात दिले आहे.
| आकार | क्षेत्र (चौरस एकके) | परिमिती (एकके) |
|---|---|---|
| चौरस
(Square) |
बाजू²
(Side)² |
4 × बाजू
(4 × Side) |
| आयत
(Rectangle) |
लांबी × रुंदी
(Length × Width ) |
2 (लांबी + रुंदी)
2 (l + b) |
| वर्तुळ
(Circle) |
त्रिज्या²
(Radius²) |
2 π त्रिज्या
2 π Radius |
| स्केलिन त्रिकोण
(Scalene Triangle) |
√ [s (s − a) (s − b) (s − c)],
जेथे, s = (a+b+c)/2 (a- त्रिकोणाची पहिली बाजू, b- त्रिकोणाची दुसरी बाजू, c- त्रिकोणाची तिसरी बाजू ) |
a+b+c |
| समद्विभुज त्रिकोण | ½ × पाया × उंची
(½ × Base × Height) |
2 बाजू + उंची
2 Base+ Height |
| समभुज त्रिकोण | (√3/4) बाजू²
((√3/4) Side²) |
3 बाजू
3 Side |
| काटकोन त्रिकोण | ½ × पाया × उंची
(½ × Base × Height) |
पाया + कर्ण + उंची
(Base+ Hypotenuse + Height) |
| समभुज चौकोन | ½ × कर्णरेषा 1 × कर्णरेषा 2
(½ × diagonal 1 × diagonal 2) |
4 × बाजू
(4 × Side) |
| समांतरभुज चौकोन | पाया × उंची
(Base × Height) |
2 (लांबी + रुंदी)
2 (l + b) |

Economic Survey In Marathi 2023
Mensuration Formula For 3D Shapes | 3D आकारांसाठी मेन्सुरेशन फॉर्म्युला
Mensuration Formula For 3D Shapes: 3D आकारांपैकी काहींचे घनफळ (Volume), पृष्ठफळ (Total Surface Area), वक्र पृष्ठभागाचे क्षेत्रफळ (Curved Surface Area) चे सूत्र खालील तक्त्यात दिले आहे.
| आकार | घनफळ (घन एकके) | वक्र पृष्ठभाग क्षेत्र (CSA) किंवा पार्श्व पृष्ठभाग क्षेत्र (LSA) (चौरस एकके) |
एकूण पृष्ठभाग क्षेत्र (TSA) (चौरस एकके) |
|---|---|---|---|
| घन
(Cube) |
a³ | 4 a² | 6 a² |
| इष्टीकाचीती
(Cuboid) |
l × b × h | 2 h (l + b) | 2 (lb +bh +hl) |
| गोल
(Sphere) |
(4/3) π r³ | 4 π r² | 4 π r² |
| `अर्धगोल
(Hemisphere) |
(⅔) π r³ | 2 π r² | 3 π r² |
| सिलेंडर
(Cylinder) |
π r² h | 2π r h | 2πrh + 2πr² |
| कोन
(Cone) |
(⅓) π r² h | π r l | πr (r + l) |
वर दिलेल्या तक्त्यात a – बाजू (Side), l – लांबी (Length), b – रुंदी (Width), h – उंची (Height), r – त्रिज्या (Radius) असा अर्थ घ्यावा.
Mensuration Formulas In Detail | तपशीलवार मेन्सुरेशन फॉर्म्युला
Mensuration Formulas In Detail: खाली दिलेल्या आकृत्यांवरून आपणास मेन्सुरेशन (Mensuration) मधील विविध आकार व त्यांचे फॉर्म्युला (Mensuration Formula) समजण्यास मदत होईल.





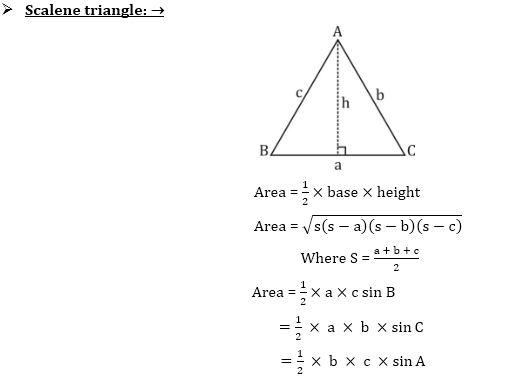
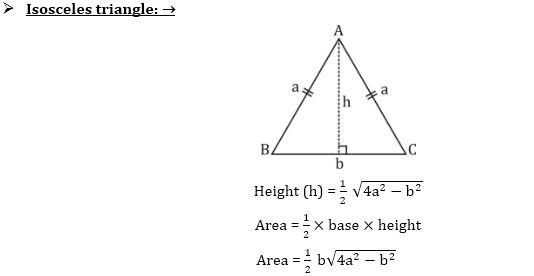
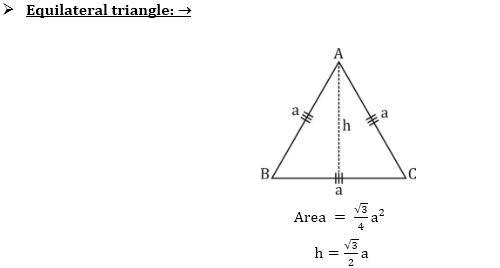
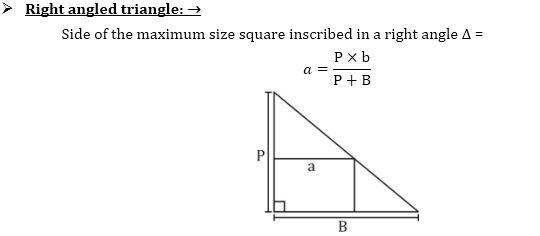
Mensuration Questions | मेन्सुरेशन प्रश्न
Mensuration Questions: पेपर मध्ये मेन्सुरेशन (Mensuration) प्रश्न कसे सोडवायचे याचा सराव होण्यसाठी काही प्रश्न व त्यांची उत्तरे खाली दिलेली आहेत.
Q1. सिलेंडरची त्रिज्या 10 सेमी आणि उंची 4 सेमी आहे. सिलेंडरच्या परिमाणात समान वाढ होण्यासाठी त्रिज्या किंवा उंची कितीने वाढली पाहिजे (सेमी मध्ये)?
Q1. The radius of a cylinder is 10 cm and the height is 4 cm. The number of centimeters that may be added either to the radius or to the height to get the same increase in the volume of the cylinder is?
(a) 5
(b) 4
(c) 25
(d) 16
Ans. (a)
Sol.
समजा त्रिज्या आणि उंचीमध्ये ‘a’ सेमी ने वाढ केली
π (10 +a) ²4 = π (10) ² (4 +a)
(10 +a) ²4 = 10² (4 +a)
⇒ a = 5 सेमी
Q2. 6 सेमी त्रिज्येचा एक घन गोलाकार वितळवून 8 सेमी आणि बाहेरील त्रिज्या 10 सेमी लांबीची पोकळ दंडगोलाकार नळी बनवल्या गेली. तर ट्यूबची जाडी मीटरमध्ये किती असेल?
Q2. A solid sphere of radius 6 cm is melted to form a hollow right circular cylindrical tube of length 8 cm and external radius 10 cm. The thickness of the tube in m is?
(a) 1
(b) 0.01
(c) 2
(d) 0.02
Ans.(d)
Sol.
घन गोलाचे घनफळ
= 4/3 π (6) ³ = 288π cu.cm
ट्यूबच्या धातूचे घनफळ
π (R² – r²)
जेथे R = 10 सेमी, h = 8 सेमी
r = आतील त्रिज्या
∴ π (R² -r²) × h = 288π
⇒ (100 -r²) = 36
⇒ r = 8 cm c घनची
जाडी = (10 -8) cm
= 2 cm
= 0.02 m
Q3. PQRS एक आयत आहे. बाजू PQ आणि QR चे गुणोत्तर 3:1 आहे. जर कर्ण PR ची लांबी 10 सेमी असेल तर आयताचे क्षेत्र (चौरस सेमी मध्ये) किती आहे?
Q3. PQRS is a rectangle. The ratio of the sides PQ and QR are 3:1. If the length of the diagonal PR is 10 cm, then what is the area (in cm²) of the rectangle?
(a) 15
(b) 30
(c) 45
(d) 20
Ans.(b)
Sol.
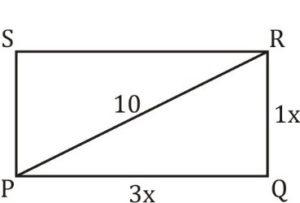
PQRS एक आयत आहे
PR = 10 (गणितात दिल्यानुसार)
PQ:QR = 3:1
∆PQR
9x² + x² = 100
10x² = 100
x = √10
आयताचे क्षेत्रफळ = 3x × 1x
= 3x²
= 3 × 10
= 30
Q4. शंकूची उंची 24 सेमी आणि पायाचे क्षेत्रफळ 154 चौरस सेमी आहे. शंकूच्या वक्र पृष्ठभागाचे क्षेत्रफळ (चौरस सेमी मध्ये) किती आहे?
Q4. The height of a cone is 24 cm and the area of the base is 154 cm². What is the curved surface area (in cm²) of the cone?
(a) 484
(b) 550
(c) 525
(d) 515
Ans.(b)
Sol.
बेसचे क्षेत्रफळ = 154
πr² = 154
22/7×r^2=154
r = 7
उंची = 24
त्रिज्या = 7
तिरकी उंची (ℓ) = √ (h²+r²)
ℓ = √ (24²+7²)
ℓ = 25
वक्र पृष्ठभागाचे क्षेत्रफळ (CSA) = πrℓ
= 22/7 × 7 × 25
वक्र पृष्ठभागाचे क्षेत्रफळ (CSA) ⇒ 550 cm²

महाराष्ट्रातील सर्व स्पर्धा परीक्षांसाठी ऑनलाईन क्लास, व्हिडिओ कोर्स, टेस्ट सिरीज, पुस्तके आणि इतर अभ्यास साहित्य खाली दिलेल्या लिंक वर क्लिक करून मिळावा.
| Latest Maharashtra Govt. Jobs | Majhi Naukri 2023 |
| Home Page | Adda 247 Marathi |
| Current Affairs in Marathi | Chalu Ghadamodi |
YouTube channel- Adda247 Marathi
Adda247 मराठी App | Add247Marathi Telegram group









