Table of Contents
आकृत्या मोजणे (Figure Counting)
आकृत्यांची मोजणी हा बुद्धिमत्ता चाचणी एक महत्वाचा टॉपिक आहे. आकृत्यांची गणना किंवा मोजणी तर्कसंगत प्रश्न हा असा प्रश्न आहे ज्यामध्ये दोन किंवा अधिक प्रकारच्या जटिल आकृत्यांच्या मिश्रणाचा समावेश होतो. यात त्रिकोण, चौरस, आयत, वर्तुळ, सरळ रेषा इत्यादी भौमितीय आकृतीचे विविध आकार समाविष्ट आहेत. या लेखात आकृत्यांच्या मोजणीचे प्रकार, प्रश्न सोडवण्यासाठी टिपा आणि युक्त्या, आणि सोडवलेली उदाहरणे दिले आहेत.
MPSC परीक्षा 2024 : अभ्यास साहित्य प्लॅन पाहण्यासाठी येथे क्लिक करा
MPSC राजपत्रित नागरी सेवा संयुक्त पूर्व परीक्षा 2024 अधिसुचना पाहण्यासाठी येथे क्लिक करा
आकृत्या मोजणे: विहंगावलोकन
यात दिलेल्या जटिल आकृतीमध्ये भौमितिक आकृत्यांच्या संख्येच्या मोजणीशी संबंधित समस्यांचा समावेश आहे. जटिल आकृतीचे विश्लेषण करून कोणत्याही विशिष्ट प्रकारच्या आकृतीची संख्या निश्चित करण्याची पद्धतशीर पद्धत खाली लेखात दिलेल्या उदाहरणांवरून स्पष्ट होईल. खालील तक्त्यात आपण आकृत्या मोजणे (Figure Counting) बद्दल विहंगावलोकन पाहू शकता.
| आकृत्या मोजणे: विहंगावलोकन | |
| श्रेणी | अभ्यास साहित्य |
| उपयोगिता | MPSC भरती परीक्षा 2024 व सर्व स्पर्धा परीक्षांसाठी |
| विषय | बुद्धिमत्ता चाचणी |
| टॉपिकचे नाव | आकृत्या मोजणे |
| महत्वाचे मुद्दे |
|
आकृत्यांच्या मोजणीचे प्रकार
स्पर्धा परीक्षेत बुद्धिमत्ता चाचणी मध्ये विचारले जाणारे आकृत्या मोजण्याचे 4 प्रकार आहेत, आकृत्यांच्या मोजणीचे प्रकार खाली दिले आहेत.
- त्रिकोणांची मोजणी
- आयतांची मोजणी
- चौरसांची मोजणी
- सरळ रेषांची मोजणी
आकृत्या मोजणीचे प्रश्न सोडवण्यासाठी टिपा आणि युक्त्या
खालील आम्ही त्रिकोणांची, आयतांची आणि चौरसांची मोजणी करण्यासाठी आवश्यक टिपा आणि युक्त्या दिल्या आहेत.
त्रिकोणांची संख्या मोजण्याची युक्ती
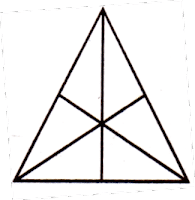
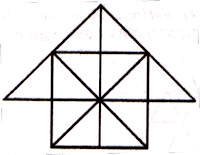
1. खाली त्रिकोण आकृती दर्शविल्याप्रमाणे, आकृती 4 भागांमध्ये विभागली आहे. परंतु कधीकधी ते 6 किंवा 8 भागात देखील विभाजित केली जाऊ शकते. तर या प्रकारच्या प्रश्नामध्ये, त्रिकोण मोजण्यासाठी सोपी युक्ती तुम्हाला माहित असली पाहिजे.
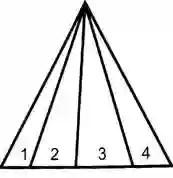
अश्या आकृतीत, आकृतीत दिल्या प्रमाणे प्रथम त्रिकोण क्रमांक लिहा, नंतर ही सोपी पद्धत लागू करा
म्हणजे 1 + 2 + 3 + 4 = 10
तर, त्रिकोणांची एकूण संख्या 10 आहे.
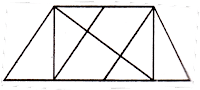
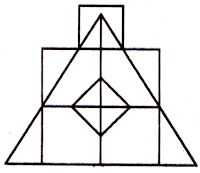
2. त्रिकोणाची आकृती खाली दर्शविल्याप्रमाणे, जी काही भागांमध्ये विभागली गेली आहे आणि या प्रकरणात काही उंची देखील विभाजित केली आहे.
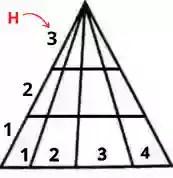
=(त्रिकोण भागाची बेरीज) x सर्वोच्च उंची भाग क्रमांक
= (1 + 2 + 3 + 4) x 3
= 30
त्यामुळे, त्रिकोणांची एकूण संख्या 30 आहे.
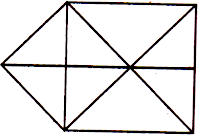
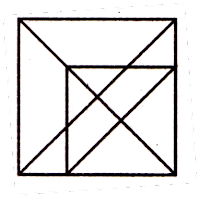
3. खालील आकृतीत दर्शविल्याप्रमाणे, आयत किंवा चौरसातील त्रिकोणांची संख्या खाली दिल्याप्रमाणे मोजता येतात.
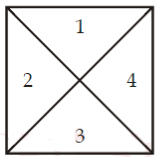
त्रिकोणांची संख्या = 4 × 2 = 8
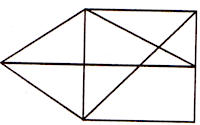
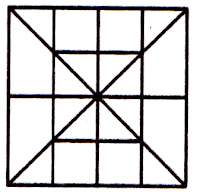
त्याचप्रमाणे, दिलेल्या चौकोनातील त्रिकोणाची संख्या खालीलप्रमाणे मोजता येतात.
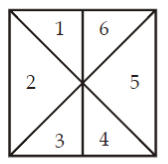
त्रिकोणांची संख्या = 6 × 2 = 12
आयतांची संख्या मोजण्याची युक्ती
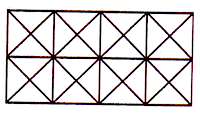
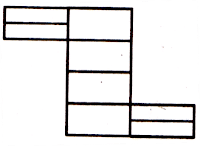
आकृती खाली दर्शविल्याप्रमाणे, आयता प्रकारातील प्रश्नामध्ये पंक्ती आणि स्तंभांची संख्या असते. त्यामुळे अशावेळी या युक्त्या लागू करा.
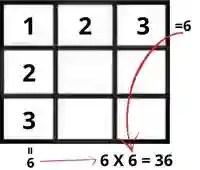
स्तंभ क्रमांक जोडणे
म्हणजे 1 + 2 + 3 = 6
पंक्ती क्रमांक जोडणे
म्हणजे 1 + 2 + 3 = 6
तर, आयतांची एकूण संख्या
6 x 6 = 36
[ही युक्ती (पंक्ती आणि स्तंभांची समान आणि भिन्न संख्या) दोन्ही स्थितींमध्ये लागू आहे]
चौरसांची संख्या मोजण्याची युक्ती
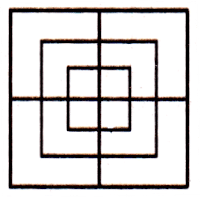
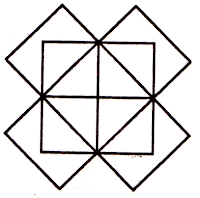
खाली आकृती दर्शविल्याप्रमाणे, जर चौरस प्रकारातील प्रश्नात समान संख्येच्या पंक्ती आणि स्तंभ असतील. तर, अशा परिस्थितीत, खालील युक्त्या लागू करा.

N = n2 + (n – 1)2 + (n – 2)2 …..
त्यामुळे चौरसांची संख्या = 32 + 22 + 12 = 9 + 4 + 1 = 14
आकृत्यांच्या मोजणीवर सोडवलेली उदाहरणे
(a) 5
MPSC भरती परीक्षा 2024 अभ्यास साहित्य
| Topic | Link |
| वेन आकृत्या | Link |
| सरासरी | Link |
| गहाळ पद शोधणे | Link |
| भागीदारी |
Link |
| असमानता | Link |
| चक्रवाढ व्याज | Link |
Note: महाराष्ट्रातील सर्व स्पर्धा परीक्षांसाठी ऑनलाईन क्लास, व्हिडिओ कोर्स, टेस्ट सिरीज, पुस्तके आणि इतर अभ्यास साहित्य खाली दिलेल्या लिंक वर क्लिक करून मिळावा.
अड्डा 247 मराठीचे युट्युब चॅनल
अड्डा 247 मराठी अँप | अड्डा 247 मराठी टेलिग्राम ग्रुप