Top 20 Arithmetic MCQs For OSSC LTR Teachers 29 November 2024

Preparing for the Odisha Staff Selection Commission (OSSC) LTR Teacher exam requires a solid understanding of basic arithmetic concepts. Here is a carefully curated list of the top 20 Multiple Choice Questions (MCQs) to help you ace the arithmetic section of the exam.

Top 20 Arithmetic MCQs For OSSC LTR Teacher

Q1. The ratio of A’s saving to that of his income is 1:5. If his expenditure on clothes increases from 20% to 27.5% with respect to his income, then what percentage of his saving is his current expenditure on clothes (assuming saving remains the same)?
(a) 127.5%
(b) 137.5%
(c) 125%
(d) 140%
Answer: (b) 137.5%
Solution:
Let A’s income be 5x.
Savings =x.
Old expenditure on clothes = 20% of 5x=x.
New expenditure on clothes = 27.5% of
5x=1.375x.
Percentage of saving spent on clothes = 1.375x*x *100=137.5.
Q2. In a class, the number of boys is 36 more than the number of girls. If 22 girls and 6 boys take admission, the ratio of girls to boys becomes 7:9. Find the original number of students in the class.
(a) 134
(b) 124
(c) 132
(d) 128
Answer: (c) 132

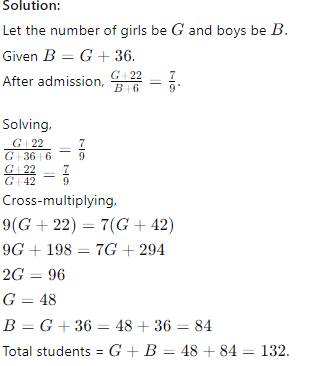
Q3. The ratio of the present age of A to that of C is 3:4. The average of the present ages of B and C is 4 years more than the present age of A. If 14 years later, A will be eight years older than B, then find the sum of the present ages of A, B, and C.
(a) 152 years
(b) 138 years
(c) 144 years
(d) 148 years
Answer: (a) 152 years
Solution:
Let A’s age be 3x and C’s age be 4x.
Average age of B and C = B+4x =3x+4
B+4x=6x+8
B=2x+8.
14 years later,
3x+14=(2x+8)+14+8
3x+14=2x+30
x=16.
Sum of present ages = 3x+2x+8+4x=9x+8
=9(16)+8=144+8=152.

Q4. Deepak and Ayush entered into a partnership by investing Rs. x and x+5000 respectively. After 6 months, Deepak increased his investment by Rs. 2000. Find the sum of their initial investments if, at the end of the year, the ratio of their profit shares is 4:5.
(a) Rs. 30000
(b) Rs. 36000
(c) Rs. 41000
(d) Rs. 35000
Answer: (d) Rs. 35000
Solution:
Deepak’s investment for 6 months = x×6.
Deepak’s investment for next 6 months = (x+2000)×6.
Ayush’s investment for 12 months = (x+5000)×12.
Total investment of Deepak = 6x+6(x+2000)=12x+12000.
Total investment of Ayush = 12(x+5000)=12x+60000.
Given, the profit ratio = 4:5
(12x+60000)/(12x+12000) = 4/5
Cross-multiplying,
5(12x+12000)=4(12x+60000)
60x+60000=48x+240000
12x=180000
x=15000.
Sum of their initial investments = x+(x+5000)=15000+20000=35000.

Q5. There are two squares with perimeters of 220 cm and 180 cm respectively. Find the perimeter of another square whose area is equal to the difference between the areas of the above two squares.
(a) 40√5 cm
(b) 40√10 cm
(c) 60√10 cm
(d) 20√10 cm
Answer: (b) 40√10 cm
Solution:
Side of first square = 220/4 =55 cm.
Area of first square = 55^2 =3025 sq. cm.
Side of second square = 180/4 =45 cm.
Area of second square = 45^2 =2025 sq. cm.
Difference in areas = 3025−2025=1000 sq. cm.
Side of the new square = Sq rt of1000=10 rt 10
Perimeter of the new square = 4*10 rt 10=40rt 10

Q6. A train running at the speed of 108 km/hr crosses a 640 meters long platform in 100/3 seconds. Find the time taken by the train to cross a man running at the speed of 36 km/hr in the opposite direction.
(a) 9 sec
(b) 12 sec
(c) 15 sec
(d) 8 sec
Answer: (a) 9 sec
Solution:
Speed of train = 108 km/hr = 108 × 5/18 m/s = 30 m/s.
Speed of man = 36 km/hr = 36 × 5/18 m/s = 10 m/s.
Relative speed (since they are moving in opposite directions) = 30 + 10 = 40 m/s.
Length of train = Speed × Time = 30 ×100/3 = 1000 m.
Time taken to cross the man = 1000/40= 25 sec.
Q7. The average weight of a class of 45 girls is 53 kg. It was later found that the weight of two girls was read as 49 kg and 57 kg instead of 45 kg and 52 kg. Find the actual average weight of the class.
(a) 54 kg
(b) 53.40 kg
(c) 50.6 kg
(d) 52.80 kg
Answer: (d) 52.80 kg
Solution:
Incorrect total weight = 45 × 53 = 2385 kg.
Correction: (45 + 52) – (49 + 57) = 97 – 106 = -9 kg.
Correct total weight = 2385 – 9 = 2376 kg.
Actual average weight = 2376/45= 52.80 kg.
Q8. In a new year offer, Axis bank reduced the interest rate from 20% to 10% per annum on C.I. Due to this offer, Anurag has to pay Rs. 345 less interest in two years. Find the loan amount of Anurag.
(a) Rs. 1,000
(b) Rs. 2,400
(c) Rs. 4,000
(d) Rs. 1,500
Answer: (d) Rs. 1,500
Solution:
Let the loan amount be P.
Interest difference over two years = P((1+(20/100)^2-1)-(1+(10/100)^2-1)=345
P(1.44-1.21)=345
Solving this, P=1500
Q9. A bag contains 4 yellow and x red balls. If 2 balls are drawn at random, the probability that both are red is 1/3. Find the value of x.
(a) 8
(b) 6
(c) 4
(d) 5
Answer: (b) 6
Solution:

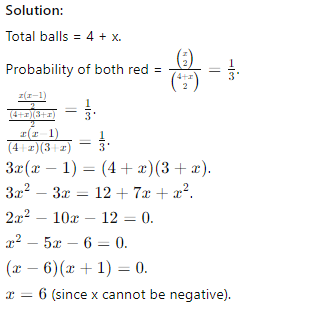
Q10. The sum of 30% of 𝑥 and 45% y is equal to zero, and the difference between 60% of x and 20% of y is equal to 22. Then find the sum of
x and y.
(a) 25
(b) 15
(c) 10
(d) 30
Answer: (c) 10
Solution:
0.3x+0.45y=0⇒3x+4.5y=0⇒6x+9y=0 (1).
0.6x−0.2y=22⇒3x−y=110 (2).
From (1),
6x+9y=0
x=−1.5y
Substituting into (2):
3(−1.5y)−y=110⇒−4.5y−y=110⇒−5.5y=110⇒y=−20.
x=−1.5(−20)=30.
Sum x+y=30+(−20)=10.

Q11. A and B started a business with investments of Rs. 30,000 and Rs. 45,000 respectively. After 6 months, A invested an additional Rs. 10,000. If the total profit at the end of the year was Rs. 20,000, find A’s share of the profit.
(a) Rs. 8750
(b) Rs. 7,500
(c) Rs. 9,000
(d) Rs. 10,000
Answer: (a) Rs. 8750
Solution:
A’s investment for the first 6 months = 30,000 × 6.
A’s investment for the next 6 months = 40,000 × 6.
B’s investment for the entire year = 45,000 × 12.
Total investment ratio = (30,000 × 6 + 40,000 × 6) : (45,000 × 12) = 420,000 : 540,000 = 7:9.
A’s share of the profit = 7/16* ×20000=8750.
Q12. C and D start a business with investments of Rs. 40,000 and Rs. 50,000 respectively. After 4 months, C withdrew Rs. 10,000 and D invested an additional Rs. 10,000. If the total profit at the end of the year was Rs. 22,000, find D’s share of the profit.
(a) Rs. 12,000
(b) Rs. 13,200
(c) Rs. 14,000
(d) Rs. 15,000
Answer: (b) Rs. 13,200
Solution:
C’s investment for the first 4 months = 40,000 × 4.
C’s investment for the next 8 months = 30,000 × 8.
D’s investment for the first 4 months = 50,000 × 4.
D’s investment for the next 8 months = 60,000 × 8.
Total investment ratio = (40,000 × 4 + 30,000 × 8) : (50,000 × 4 + 60,000 × 8) = 400,000 : 600,000 = 2:3.
D’s share of the profit = 3/5×22000=13200

Q13. E, F, and G enter into a partnership with investments in the ratio 2:3:5. After 4 months, E withdraws half of his investment. If the total profit at the end of the year is Rs. 48,000, what is G’s share of the profit?

(a) Rs. 24,000
(b) Rs. 30,000
(c) Rs. 36,000
(d) Rs. 40,000
Answer: (b) Rs. 30,000
Solution:
E’s initial investment for 4 months = 2x × 4.
E’s investment for the next 8 months = x × 8.
F’s investment for the entire year = 3x × 12.
G’s investment for the entire year = 5x × 12.
Total investment ratio = (8x + 8x) : (36x) : (60x) = 16 : 36 : 60 = 4:9:15.
G’s share of the profit = 15/28×48000=30000

Q14. H and I invested Rs. 50,000 and Rs. 70,000 respectively in a business. J joined them after 6 months with an investment of Rs. 80,000. If the profit at the end of the year was Rs. 25,000, what is I’s share of the profit?
(a) Rs. 8,000
(b) Rs. 10,000
(c) Rs. 12,000
(d) Rs. 15,000
Answer: (a) Rs. 8,000
Solution:
H’s investment for the entire year = 50,000 × 12.
I’s investment for the entire year = 70,000 × 12.
J’s investment for the last 6 months = 80,000 × 6.
Total investment ratio = (50,000 × 12) : (70,000 × 12) : (80,000 × 6) = 600,000 : 840,000 : 480,000 = 5:7:4.
I’s share of the profit = 7/16*25000=8750.
Q15. K, L, and M enter into a partnership. K invests Rs. 60,000, L invests Rs. 80,000, and M invests Rs. 100,000. After 8 months, M withdraws Rs. 40,000. If the profit at the end of the year is Rs. 36,000, what is K’s share of the profit?
(a) Rs. 9,000
(b) Rs. 12,000
(c) Rs. 15,000
(d) Rs. 18,000
Answer: (a) Rs. 9,000
Solution:
K’s investment for the entire year = 60,000 × 12.
L’s investment for the entire year = 80,000 × 12.
M’s investment for the first 8 months = 100,000 × 8.
M’s investment for the last 4 months = 60,000 × 4.
Total investment ratio = (60,000 × 12) : (80,000 × 12) : (800,000 + 240,000) = 720,000 : 960,000 : 1,040,000 = 18:24:26.
K’s share of the profit = 18/68×36000=9000

Q16. The average of five numbers is 60. If one number is excluded, the average becomes 55. What is the excluded number?
(a) 65
(b) 70
(c) 75
(d) 80
Answer: (d) 80
Solution:
Sum of five numbers = 5 × 60 = 300.
Sum of the remaining four numbers = 4 × 55 = 220.
Excluded number = 300 – 220 = 80.
Q17. The average age of a group of 12 students is 20 years. If 3 students with an average age of 24 years leave the group, what is the average age of the remaining students?
(a) 18.5 years
(b) 19 years
(c) 20.5 years
(d) 21 years
Answer: (a) 18.5 years
Solution:
Total age of 12 students = 12 × 20 = 240 years.
Total age of 3 students = 3 × 24 = 72 years.
Total age of remaining 9 students = 240 – 72 = 168 years.
Average age of remaining students = 168/9=18.67
Q18. The average marks of 30 students in a class is 75. If the marks of five students were incorrectly entered as 60, 65, 70, 75, and 80 instead of 70, 75, 80, 85, and 90 respectively, what is the correct average?
(a) 76.5
(b) 77
(c) 77.5
(d) 78
Answer: (c) 77.5
Solution:
Incorrect total marks = 30 × 75 = 2250.
Correct total marks for the five students = 70 + 75 + 80 + 85 + 90 = 400.
Incorrect total marks for the five students = 60 + 65 + 70 + 75 + 80 = 350.
Correct total marks = 2250 + (400 – 350) = 2300.
Correct average = 2300/30=76.67
Q19. The average of 7 consecutive even numbers is 20. What is the smallest of these numbers?
(a) 16
(b) 18
(c) 20
(d) 22
Answer: (b) 18
Solution:
Let the seven consecutive even numbers be
x−6,x−4,x−2,x,x+2,x+4,x+6.
Their average = 20.
(x−6)+(x−4)+(x−2)+x+(x+2)+(x+4)+(x+6)​ =20.
solving this
x=20.
The smallest number is
x−2=20−2=18.

Q20. The average age of a family of 5 members is 30 years. If the youngest member is 10 years old, what was the average age of the family at the time of the birth of the youngest member?
(a) 20 years
(b) 24 years
(c) 26 years
(d) 28 years
Answer: (a) 20 years
Solution:
Total age of the family = 5 × 30 = 150 years.
10 years ago, the total age of the family was 150 – (10 × 5) = 100 years.
Number of family members = 5.
Average age 10 years ago = 100/5=20 years.

Q21. The length of a rectangular field is twice its breadth. If the perimeter of the field is 240 meters, find the length of the field.
(a) 60 meters
(b) 80 meters
(c) 100 meters
(d) 120 meters
Answer: (c) 80 meters
Solution:
Let the breadth be x meters.
Then, length = 2x meters.
Perimeter = 2(length + breadth) = 240 meters.
2(2x + x) = 240.
6x = 240.
x = 40 meters.
Length = 2x = 80 meters.
Q22. The radius of a circular garden is 14 meters. Find the area of the garden.
(a) 616 sq. meters
(b) 308 sq. meters
(c) 792 sq. meters
(d) 588 sq. meters
Answer: (a) 616 sq. meters
Solution:
Area of the circle = πr^2.
Area= 22/7×14×14=616 sq. meters.
Q23. A cylindrical tank has a diameter of 10 meters and a height of 15 meters. Find the volume of the tank.
(a) 1177 cubic meters
(b) 1250 cubic meters
(c) 1500 cubic meters
(d) 2000 cubic meters
Answer: (a) 1177 cubic meters
Solution:
Volume of the cylinder = πr^2h.
= 22/7×5^2×15
=1177 cubic meters.
Q24. The base of a triangular field is 20 meters and its height is 15 meters. Find the area of the field.
(a) 150 sq. meters
(b) 200 sq. meters
(c) 250 sq. meters
(d) 300 sq. meters
Answer: (a) 150 sq. meters
Solution:
Area of the triangle = 1/2×base×height​=
1/2×20×15=150 sq. meters.
Q25. A cube has a side length of 8 cm. Find the surface area of the cube.
(a) 256 sq. cm
(b) 384 sq. cm
(c) 512 sq. cm
(d) 64 sq. cm
Answer: (b) 384 sq. cm
Solution:
Surface area of the cube = 6a^2.
= 6 × 8^2 = 6 × 64 = 384 sq. cm.

Q26. The 5th term of an arithmetic progression (AP) is 20 and the 10th term is 35. Find the common difference of the AP.
(a) 2
(b) 3
(c) 4
(d) 5
Answer: (a) 3

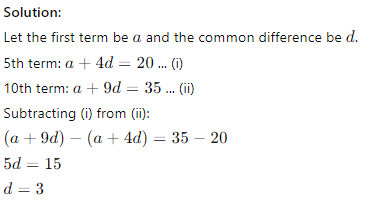
Q27. The sum of the first 10 terms of an arithmetic progression (AP) is 150. If the first term is 5, find the common difference.
(a) 2
(b) 3
(c) 4
(d) 5
Answer: (a) 2

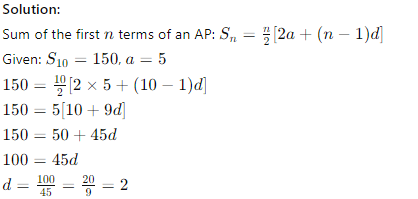
Q28. In a geometric progression (GP), the first term is 3 and the common ratio is 2. Find the 6th term of the GP.
(a) 32
(b) 48
(c) 64
(d) 96
Answer: (c) 96

Q29. The sum of the first 5 terms of a geometric progression (GP) is 62 and the common ratio is 2. Find the first term.
(a) 1
(b) 2
(c) 3
(d) 4
Answer: (b) 2

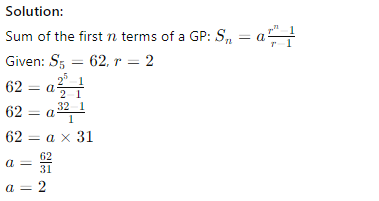
Q30. If the 4th term of an arithmetic progression (AP) is 10 and the 8th term is 22, find the first term.
(a) 1
(b) 2
(c) 3
(d) 4
Answer: (a) 1