Mathematics is an integral part of various competitive exams, including the OSSSC (Odisha Subordinate Staff Selection Commission) RI (Revenue Inspector), ARI (Assistant Revenue Inspector), Amin, SFS, and ICDS Supervisor exams. To excel in these exams, candidates need to have a solid understanding of mathematical concepts and problem-solving skills. To help you prepare effectively, we’ve compiled a list of the top 30 Mathematics Multiple Choice Questions (MCQs) commonly encountered in these exams.
Top 30 Mathematics MCQs For OSSSC RI,ARI, Amin, SFS, ICDS Supervisor
- There are two circles of different radii. The area of a square is 196 sq.cm, whose side is half the radius of the larger circle. The radius of the smaller circle is three-seventh that of the larger circle. What is the circumference of the smaller circle?
A. 12π cm
B. 16π cm
C. 24π cm
D. 32π cm
Answer: C. 24π cm
Sol: Side of the square = √196 = 14 cm
Radius of the larger circle = 2 * 14 = 28 cm
Radius of the smaller circle = (3/7) * 28 = 12 cm
Circumference of the smaller circle = 2π * 12 = 24π cm - The perimeter of a square is equal to the perimeter of a rectangle of length 16 cm and breadth 14 cm. Find the circumference of a semicircle whose diameter is equal to the side of the square. (Round off your answer to two decimal places).
A. 23.57 cm
B. 47.14 cm
C. 84.92 cm
D. 94.94 cm
Answer: A. 23.57 cm
Solution:
Perimeter of the rectangle = 2(16 + 14) = 60 cm
Perimeter of the square = 60 cm
Side of the square = 60 / 4 = 15 cm
Diameter of the semicircle = 15 cm
Circumference of the semicircle = (1/2)π * 15 + 15 = (1/2)(22/7) * 15 = 23.57 cm - A 25 cm wide path is to be made around a circular garden having a diameter of 4 meters. Approximate area of the path in square meters is:
A. 3.34
B. 2
C. 4.5
D. 5.5
Answer: A. 3.34
Solution:
Radius of the inner circle = 4/2 = 2 meters
Radius of the outer circle = 2 + 0.25 = 2.25 meters
Area of the path = π(2.25² – 2²) = π(5.0625 – 4) = π(1.0625) = 3.34 sq meters - A cuboidal block of 6 cm X 9 cm X 12 cm is cut up into an exact number of equal cubes. The least possible number of cubes will be:
A. 6
B. 9
C. 24
D. 30
Answer: C. 24
Solution:
Volume of the block = 6 * 9 * 12 = 648 cm³
Side of the largest cube = H.C.F. of 6, 9, and 12 = 3 cm
Volume of one cube = 3³ = 27 cm³
Number of cubes = 648 / 27 = 24 - I. 9a2 + 18a + 5 = 0,
II. 2b2 + 13b + 20 = 0 to solve both the equations to find the values of a and b?
A. If a > b
B. If a ≥ b
C. If a < b
D. If a ≤ b
Ans: A. If a > b
Explanation:
I. 9a2 + 3a + 15a + 5 = 0
=>(3a + 5)(3a + 1) = 0 => a = -5/3, -1/3
II. 2b2 + 8b + 5b + 20 = 0
=>(2b + 5)(b + 4) = 0 => b = -5/2, -4
a is always more than b.
a > b. - I. x2 + 9x + 20 = 0,
II. y2 + 5y + 6 = 0 to solve both the equations to find the values of x and y?
A. If x < y
B. If x > y
C. If x ≤ y
D. If x ≥ y
Ans: A. If x < y
I. x2 + 4x + 5x + 20 = 0
=>(x + 4)(x + 5) = 0 => x = -4, -5
II. y2 + 3y + 2y + 6 = 0
=>(y + 3)(y + 2) = 0 => y = -3, -2
= x < y. - 9000 + 16 2/3 % of ? = 10500
A. 1500
B. 1750
C. 9000
D. 7500
Ans: C. 9000
Explanation:
9000 + 16 2/3 % of ? = 10500 => 9000 + 50/3 % of ? = 10500
50/(3 * 100) of ? = 1500 => ? = 1500 * 6
? = 9000 - Two pipes A and B can fill a cistern in 37 1/2 minutes and 45 minutes respectively. Both pipes are opened. The cistern will be filled in just half an hour, if the pipe B is turned off after?
A. 5 min
B. 9 min
C. 10 min
D. 15 min
Ans: B. 9 min
Explanation:
Let B be turned off after x minutes. Then, part filled by (A + B) in x min + part filled by A in (30 – x) min = 1.
x(2/75 + 1/45) + (30- x) 2/75 = 1
11x + 180 – 6x = 225 => x = 9 - Two pipes can fill a tank in 20 and 24 minutes respectively and a waste pipe can empty 3 gallons per minute. All the three pipes working together can fill the tank in 15 minutes. The capacity of the tank is?
A. 60 gallons
B. 100 gallons
C. 120 gallons
D. 180 gallons
Ans: C. 120 gallons
Explanation:
Work done by the waste pipe in 1 minute = 1/15 – (1/20 + 1/24) = – 1/40
Volume of 1/40 part = 3 gallons\
Volume of whole = 3 * 40 = 120 gallons. - I. a3 – 988 = 343,
II. b2 – 72 = 49 to solve both the equations to find the values of a and b?
A. If a > b
B. If a ≥ b
C. If a < b
D. If a ≤ b
Ans: B. If a ≥ b
Explanation:
a3 = 1331 => a = 11
b2 = 121 => b = ± 11
a ≥ b - Which of the equations below doesn’t qualify the criteria of a quadratic equation?
A. (x + 2)2 = 2(x + 3)
B. x2 + 3x = (–1) (1 – 3x)2
C. (x + 2) (x – 1) = x2 – 2x – 3
D. x3 – x2 + 2x + 1 = (x + 1)3
Ans. (c) (x + 2) (x – 1) = x2 – 2x – 3
Explanation: We know that a quadratic equation has a degree of two.
By double-checking the selections,
(a) (x + 2)2 = 2(x + 3)
x2 + 4x + 4 = 2x + 6
x2 + 2x – 2 = 0
Thus, This is an example of a quadratic equation.
(b) x2 + 3x = (–1) (1 – 3x)2
x2 + 3x = -1(1 + 9×2 – 6x)
x2 + 3x + 1 + 9×2 – 6x = 0
10×2 – 3x + 1 = 0
Thus, This is an example of a quadratic equation.
(c) (x + 2) (x – 1) = x2 – 2x – 3
x2 + x – 2 = x2 – 2x – 3
x2 + x – 2 – x2 + 2x + 3 = 0
3x + 1 = 0
This is not an example of a quadratic equation. - 11th term of the A.P. -3, -1/2, 2 …. is
A. 28
B. 22
C. -38
D. -48
Ans. (b) 22
Explanation: A.P. = -3, -1/2, 2 …
First-term a = – 3
Common difference, d = a2 − a1 = (-1/2) -(-3)
⇒(-1/2) + 3 = 5/2
Nth term;
an = a+(n−1)d
a11 = 3+(11-1)(5/2)
a11 = 3+(10)(5/2)
a11 = -3+25
a11 = 22 - The following words are missing from AP: __, 13, __, 3:
A. 11 and 9
B. 17 and 9
C. 18 and 8
D. 18 and 9
Ans. (c) 18 and 8
Explanation: a2 = 13 and
a4 = 3
The nth term of an AP;
an = a+(n−1) d
a2 = a +(2-1)d
13 = a+d ………………. (i)
a4 = a+(4-1)d
3 = a+3d ………….. (ii)
When we subtract equation I from equation (ii), we obtain
– 10 = 2d
d = – 5
Fill in the value of d in equation 1 now.
13 = a+(-5)
a = 18 (first term)
a3 = 18+(3-1)(-5)
= 18+2(-5) = 18-10 = 8 (third term). - ∠B = ∠E, ∠F = ∠C and AB = 3 DE in triangles ABC and DEF. The two triangles are
A. congruent but not similar
B. similar but not congruent
C. neither similar nor congruent
D. similar as well as congruent
Ans. (b) similar but not congruent
Explanation: In ΔABC and ΔDEF,
∠B = ∠E, ∠F = ∠C and AB = 3 DE
By AA similarity criterion,
ΔABC ~ ΔDEF
AB = 3DE
⇒ AB/DE = 3
⇒ AB/DE = BC/EF = AC/DF = 3
Triangles must have a side ratio of 1 to be congruent.
Therefore, triangles are similar but not congruent. - ΔABC ~ ΔDFE, ∠A = 30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm are provided. If that’s the case, then the following is correct:
A. DE = 12 cm, ∠ F = 50 degrees
B. DE = 12 cm, ∠ F = 100 degrees
C. ∠D = 100°, EF = 12 cm
D. ∠D = 30°, EF = 12 cm
Ans. (b) DE = 12 cm, ∠F = 100°
Explanation: Given,
ΔABC ~ ΔDFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF= 7.5 cm
In triangle ABC,
∠A + ∠B + ∠C = 180°
∠B = 180° – 30° – 50° = 100°
The corresponding angles are equivalent because ΔABC ~ ΔDFE,
Thus, ∠D = ∠A = 30°
∠F = ∠B = 100°
∠E = ∠C = 50°
And
AB/DF = AC/DE
5/7.5 = 8/DE
DE = (8 × 7.5)/5 = 12 cm - A triangle with vertices (a, b + c), (b, c + a), and (c, a + b) has an area of :
A. (a + b + c)2
B. 0
C. a + b + c
D. ab
Ans. (b) 0
Explanation: Let the triangle’s vertices be:
A = (x1, y1) = (a, b + c)
B = (x2, y2) = (b, c + a)
C = (x3, y3) = (c, a + b)
Area of triangle ABC = (1/2)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
= (1/2)[a(c + a – a – b) + b(a + b – b – c) + c(b + c – c – a)]
= (1/2)[a(c – b) + b(a – c) + c(b – a)]
= (1/2)[ac – ab + ab – bc + bc – ac]
= (1/2)(0)
= 0 - The expression sin6θ + cos6θ + 3 sin2θ cos2θ has a value of:-
A. 0
B. 3
C. 2
D. 1
Ans. (d) 1
Explanation: We know that, sin2θ + cos2θ = 1
Taking cube on both sides,
(sin2θ + cos2θ)3 = 1
(sin2θ)3 + (cos2θ)3 + 3 sin2θ cos2θ (sin2θ + cos2θ) = 1
sin6θ + cos6θ + 3 sin2θ cos2θ = 1 - The bucket’s two-round ends have sizes of 44 cm and 24 cm. The bucket stands 35 centimetres tall. The bucket has a capacity of
A. 32.7 litres
B. 33.7 litres
C. 34.7 litres
D. 31.7 litres
Ans. (a) 32.7 litres
Explanation: Given,
The bucket’s height is h = 35 cm.
One bucket’s circular end has a diameter of 44 cm.
The radius R = 22 cm is then calculated.
Another end’s diameter is 24 cm.
The radius r = 12 cm is then calculated.
We know that Volume of the bucket = (1/3)πh[R2 + r2 + Rr]
= (1/3) × (22/7) × 35 × [(22)2 + (12)2 + 22 × 12]
= (35/3) × (22/7) × (484 + 144 + 264)
= (5 × 22 × 892)/3
= 32706.6 cm3
= 32.7 litres. - The probability of a non-leap year with 53 Sundays being chosen at random is
A. 1/7
B. 2/7
C. 3/7
D. 5/7
Ans. (a) 1/7
Explanation: Non-leap year = 365 days
52 weeks Plus 1 day Equals 365 days
The number of Sundays in a 52-week period equals 52.
Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, and Sunday are all possible options for the last day.
The total number of possible outcomes: 7.
1 is the number of positive results.
As a result, the chance of receiving 53 Sundays is 1/7. - At what point does the perpendicular bisector of the line segment joining the points A(1,5) and B(4,6) cut the y-axis?
A. (0, 13)
B. (0, –13)
C. (0, 12)
D. (13, 0)
Ans. (a) (0, 13)
Explanation: The perpendicular bisector of line segment AB, as we know, is perpendicular at AB and goes across AB’s midpoint.
Let P be the AB’s midpoint.
Mid – point of AB = [(1 + 4)/2, (5 + 6)/2]
P = (5/2, 11/2)
The line AB’s slope = (6 – 5)/(4 – 1) = 1/3 is now calculated.
As a result, the bisector’s slope = -1/slope of line AB = -1/(1/3) = -3.
Using the point-slope form, the equation for the line passing through the point P(5/2, 11/2) with slope -3 is:
y – (11/2) = -3[x – (5/2)]
(2y – 11)/2 = -3[(2x – 5)/2]
2y – 11 = -6x + 15
2y = -6x + 15 + 11
2y = -6x + 26
y = -3x + 13
The formula is y = mx + c.
The y-intercept is c = 13 in this case.
As a result, the y-axis is cut at A(1, 5) by the perpendicular bisector of the line segment linking the points A(1, 5) and B(4, 6). (0, 13). - The expression sin6θ + cos6θ + 3 sin2θ cos2θ has a value of:-
A. 0
B. 3
C. 2
D. 1
Ans. (d) 1
Explanation: We know that, sin2θ + cos2θ = 1
Taking cube on both sides,
(sin2θ + cos2θ)3 = 1
(sin2θ)3 + (cos2θ)3 + 3 sin2θ cos2θ (sin2θ + cos2θ) = 1
sin6θ + cos6θ + 3 sin2θ cos2θ = 1 - In a given location, it is recommended to construct a single circle park with an area equal to the total of the areas of two circular parks with diameters of 16 m and 12 m. The new park’s radius would be
A. 10 m
B. 15 m
C. 20 m
D. 24 m
Ans. (a) 10 m
Explanation: Radii of two circular parks will be:
R1 = 16/2 = 8 m
R2 = 12/2 = 6 m
Let R be the new circular park’s radius.
If the areas of two circles with radii R1 and R2 are identical, then the area of a circle with radius R is also equal.
R2 = R12 + R22
= (8)2 + (6)2
= 64 + 36
= 100
R = 10 m - The value of c for which the equations cx–y = 2 and 6x–2y = 3 have an unlimited number of solutions is
A. 3
B. -3
C. -12
D. no value
Ans. (d) no value
Explanation: cx – y = 2 and 6x – 2y = 3 are the given equations.
When compared to the conventional form,
a1 = c, b1 = -1, c1 = -2
c2= -3, a2 = 6, b2 = -2
a1/a2 = c/6
b1/b2 = -1/-2 = 1/2
c1/c2 = -2/-3 = 2/3
There must be a condition for there to be an infinite number of solutions.
a1/a2 = b1/b2 = c1/c2
c/6 = 1/2 = 2/3
Therefore,
c = 3 and c = 4
Here, c has different values.
As a result, the pair of equations will have an endless number of solutions for any value of c. - If one of the cubic polynomial’s zeroes is x3 + ax2 + bx + c, then the product of the other two zeroes is:
A. b-a-1
B. b-a+1
C. a-b+1
D. a-b-1
Ans. (b) b-a+1
Explanation: Since one zero equals -1,
P(x) = x3+ax2+bx+c
P(-1) = (-1)3+a(-1)2+b(-1)+c
0 = -1+a-b+c
c=1-a+b
-constant term/coefficient of x3= Product of zeroes, αβγ
(-1)βγ = -c/1
c=βγ
βγ = b-a+1 - MAMA can row 20 kilometres downstream in 2 hours and 4 kilometres upstream in 2 hours. Her rowing speed on calm water and the current speed is:
A. 6 km/hr and 3kph
B. 7 kph and 4 kph
C. 6 kph and 4 kph
D. 10 kph and 6 kph
Ans. (c) 6km/hr and 4km/hr
Explanation: Let’s say Mama’s speed in calm water is x km/hr.
Stream Speed = y km/hr
Now, Mama’s pace during,
Downstream = x + y km/h
Upstream = x – y km/h
As per the question given,
2(x+y) = 20
Or x + y = 10……………………….(1)
And, 2(x-y) = 4
Or x – y = 2………………………(2)
When both equations are added together, we obtain
2x=12
x = 6
When we plug in the value of x into eq.1, we obtain
y = 4
Therefore,
Mama’s speed in calm water is 6 km/hr.
Stream speed = 4 km/hr - 0.004 × 0.02 = ?
(A) 0.08
(B) 0.008
(C) 0.0008
(D) 0.00008
Ans: (D) 0.000080.004 × 0.02=
(1) 4*2= 8,
(2) 0.003 Three digits after Decimal,
0.02 Two digits after Decimal
(3) So, Five Digits After Decimal Therefore,
0.004*0.02= 0.00008 - What is the average of the numbers: 0, 0, 4, 10, 5, and 5 ?
(A) 2
(B) 3
(C) 4
(D) 5
Ans: (C) 4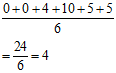
- What is the rate of discount if a car which price was $4,000 was sold for $3,200 ?
(A) 14%
(B) 16%
(C) 18%
(D) 20%
Ans: (D) 20%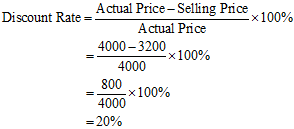
- |–2| + |2| – 2 + 2 = ?
(A) 0
(B) 2
(C) 4
(D) 8
Ans: (C) 4|–2| + |2| – 2 + 2 = ?
2+2-2+2= 4 - What is the value of x in the equation 4x – 12 – 4 =0 ?
(A) 4
(B) 8
(C) 9
(D) –9
Ans: (A) 7
4x – 12 – 4 =0
4x-16=0
4x=16
x= 16/4
= 4










