Acute angle Meaning, Definition with Diagram

Acute Angle

An angle is a figure created by two rays, called the sides of the angle, that share a common endpoint, called the vertex of the angle, in Euclidean geometry. The plane that contains the rays contains the angles formed by two beams. Angles are also generated when two planes intersect. Dihedral angles are what they’re called. Two intersecting curves can also define an angle, which is the angle formed by rays lying tangent to the curves at their junction. Acute Angle can also refer to the measurement of an angle or a rotation. The length of a circular arc divided by its radius is this measurement. The arc is centred at the vertex and defined by the sides in the case of a geometric angle. When a rotation occurs, the arc is centred at the rotation’s centre and delimited by any other point and the rotation’s image.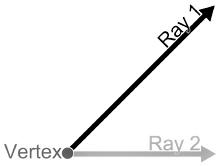

Figure: Two rays forming an angle

Acute Angle Meaning

An acute angle is a term used in geometry to describe an angle that is less than 90 degrees. In other words, an acute angle is an angle that is smaller or narrower than a right angle, which measures exactly 90 degrees. Acute angles are typically associated with sharp or narrow turns and are commonly found in various geometric shapes and everyday objects. When two lines intersect in such a way that they form acute angles at their point of intersection, the angles are often referred to as acute angles. These angles are essential in geometry and trigonometry for various calculations and measurements.

Acute Angle Definition with Diagrams

Acute Angle Definition: An acute angle is one that is less than 90 degrees. The acute angle is also known as the angle that is smaller than 90 degrees. The acute angle is represented by the symbol ⦟ and is measured in degrees using a protractor. Two lines intersect at a location to make an angle in mathematics. Acute, obtuse, right, and other forms of angles exist in geometry. An acute angle is one that is smaller than 90 degrees. Triangles, parallelograms, trapezoids, and other polygons all have at least one acute angle.

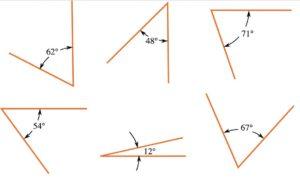
Figure: Examples of Acute Angles

Acute Angle Triangle

Triangle: A triangle is a three-sided polygon with three vertices and three edges. It is a fundamental geometric shape. Triangle XYZ is a triangle with vertices X, Y, and Z. In Euclidean geometry, any three non-collinear points form a unique triangle and, at the same time, a unique plane.

Acute Angle Triangle: An acute-angled triangle is one in which all three internal angles of the triangle are acute, meaning they are less than 90 degrees. At the same time, a triangle cannot be sharp and right-angled. A triangle cannot be both obtuse and acute at the same time. There are three types of acute angle triangle.

Acute Equilateral Triangle:

An equilateral acute triangle’s internal angles are all 60 degrees. An equi-angular triangle is another name for it.

Acute Isosceles Triangle:

An isosceles acute triangle’s two angles, like its two sides, have the same measurement. E.g. Two angles of a triangle are equal to 55 degrees each and the remaining third angle is equal to 70 degrees.

Acute Scalene Triangle:

A scalene acute triangle has three uneven sides and internal angles, all of which are less than 90 degrees. E.g. The three angles of a triangle are 50 degrees, 60 degrees and 70 degrees.

Acute Angle and Obtuse Angle

The obtuse angle is defined as any angle that is more than 90 degrees. Angles range from 90 to 180 degrees. If we have the acute angle measurement, we can calculate an obtuse angle.

The obtuse Angle triangle is also the one in which in angle of the triangle is greater than 90 degrees. The other two angles of the triangle still remain less than 90 degrees or acute angles.

Difference between Acute Angle and Obtuse Angles:

Acute Angle in Hindi

कोण दो किरणों द्वारा बनाई गई एक आकृति है, जिसे कोण की भुजाएं कहा जाता है, जो यूक्लिडियन ज्यामिति में एक सामान्य समापन बिंदु को साझा करती है, जिसे कोण का शीर्ष कहा जाता है। जिस तल में किरणें होती हैं उसमें दो किरणों द्वारा निर्मित कोण होते हैं। जब दो तल प्रतिच्छेद करते हैं तो कोण भी उत्पन्न होते हैं। डायहेड्रल कोण उन्हें कहा जाता है। दो प्रतिच्छेदी वक्र भी एक कोण को परिभाषित कर सकते हैं, जो उनके जंक्शन पर वक्रों के स्पर्शरेखा पर पड़ी किरणों द्वारा बनाया गया कोण है। न्यून कोण किसी कोण या घूर्णन के माप को भी संदर्भित कर सकता है। एक वृत्ताकार चाप की लंबाई को उसकी त्रिज्या से विभाजित करने पर यह माप प्राप्त होता है। चाप शीर्ष पर केन्द्रित होता है और ज्यामितीय कोण के मामले में भुजाओं द्वारा परिभाषित होता है। जब कोई घूर्णन होता है, तो चाप घूर्णन के केंद्र पर केंद्रित होता है और किसी अन्य बिंदु और घूर्णन की छवि द्वारा सीमांकित होता है।

न्यून कोण एक शब्द है जिसका उपयोग ज्यामिति में 90 डिग्री से कम के कोण का वर्णन करने के लिए किया जाता है। दूसरे शब्दों में, न्यून कोण वह कोण होता है जो समकोण से छोटा या संकरा होता है, जिसका माप बिल्कुल 90 डिग्री होता है। न्यून कोण आमतौर पर तीव्र या संकीर्ण घुमावों से जुड़े होते हैं और आमतौर पर विभिन्न ज्यामितीय आकृतियों और रोजमर्रा की वस्तुओं में पाए जाते हैं। जब दो रेखाएं इस तरह से प्रतिच्छेद करती हैं कि वे अपने प्रतिच्छेदन बिंदु पर न्यून कोण बनाती हैं, तो उन कोणों को अक्सर न्यून कोण कहा जाता है। ये कोण ज्यामिति और त्रिकोणमिति में विभिन्न गणनाओं और मापों के लिए आवश्यक हैं।

न्यून कोण परिभाषा: न्यून कोण वह है जो 90 डिग्री से कम होता है। न्यून कोण को 90 डिग्री से छोटा कोण भी कहा जाता है। न्यून कोण को प्रतीक ⦟ द्वारा दर्शाया जाता है और इसे चांदे का उपयोग करके डिग्री में मापा जाता है। गणित में कोण बनाने के लिए दो रेखाएँ एक स्थान पर प्रतिच्छेद करती हैं। ज्यामिति में न्यून, अधिक, समकोण और कोणों के अन्य रूप मौजूद हैं। न्यून कोण वह होता है जो 90 डिग्री से छोटा होता है। त्रिभुज, समांतर चतुर्भुज, समलम्ब चतुर्भुज और अन्य बहुभुज सभी में कम से कम एक न्यून कोण होता है।

Related Post:

• a3 B3 Formula- Proof, Solution And Examples
• Cube Formula For Area, Volume In Maths
• Planck’s Constant- Value, Definition, Unit, Symbol, Formula
• Bohr Atomic Model- Diagram, Formula, Postulates And Limitations
• Median Formula For Even, Odd, And Grouped Data

Sharing is caring!