Algebra Formulas PDF, Get All Algebraic Identities Formula Chart for Class 9

Algebra is a branch of Mathematics that substitutes letters for numbers. An algebraic equation depicts a scale, what is done on one side of the scale with a number is also done on either side of the scale. Mathematical numbers are constants. Algebra also includes real numbers, complex numbers, matrices, vectors, and much more. X, Y, A, and B are the most commonly used letters that represent algebraic problems and equations.

Algebra Formula

“Algebra Formulas form the foundation of numerous most important topics of mathematics. Topics like equations, quadratic equations, polynomials, coordinate geometry, calculus, trigonometry, and probability, extensively depend on algebraic formulas for understanding and for solving complex problems.”

Definition of Algebra Formula

This formula is part of Class 9, 10 Maths in India. One of the most crucial areas of mathematics is algebra. Numerous disciplines, including quadratic equations, polynomials, coordinate geometry, calculus, trigonometry, probability, and others, can be solved using algebraic formulas. In these formulas, we used numbers along with letters together. The most common letters used in algebraic equations and problems are X, Y, A, and B. These formulas enable us to quickly and efficiently tackle time-consuming algebraic problems. Here, we include all significant Algebraic formulas together with their solutions, so that students can access them all in one place.

Algebra Formulas Example

Algebra formulas are basically algebra equations formed by algebraic and mathematical phrases and symbols. These algebraic formulas contain an unknown variable x which can be generated while simplifying an equation. These algebraic equations solve complicated algebraic computations in an easy way.
For example,

(a+b)³ =a³+ 3a²b+3ab²+b³
In the above formulas, both sides are individually an algebraic equation. Where ( a³ + 3a²b+3ab²+b³ ) is the simplified expression of (a+b)³ .

In algebra formulas, an identity is an equation that is always fall true regardless of the values assigned to the variables. Algebraic Identity means that the left-hand side (LHS) of the equation is identical to the right-hand side (RHS) of the equation and for all values of the variables. Algebraic identities applications are in solving the values of unknown variables. Here are some commonly used algebraic identities:

Algebraic Identities Formula

• (a + b)² = a² + 2ab + b²
• (a – b)² = a² – 2ab + b²
• (a + b)(a – b) = a² – b²
• (x + a)(x + b) = x² + x(a + b) + ab

Algebra Formulas For Squares of Class 10

Here are some important formulas involving squares.
• a²– b² = (a – b)(a + b)
• (a + b)²=  a²+ 2ab + b²
• a²+ b²= (a + b)²– 2ab
• (a – b)² = a²– 2ab+ b²
• (a + b + c)² = a² + b² + c²+ 2ab + 2bc + 2ca
• (a – b – c)² = a²+ b²+ c²– 2ab + 2bc – 2ca

Algebra Formulas for Cube of SSC CGL

Here are some Algebraic formulas involving cubes.

• (a + b)³ = a³+ 3a²b + 3ab²+ b³
•  (a + b)³ = a³ + b³ + 3ab(a + b)
• (a – b)³= a³ – 3a²b + 3ab² – b³
• (a – b)³= a³ – b³ – 3ab(a – b)
• a³ – b³ = (a – b)(a²+ ab + b²)
• a³ + b³ = (a + b)(a²– ab + b²)

Some more Algebra formulas are –
• (a + b)⁴= a⁴+ 4a³b + 6a²b² + 4ab³ + b²
• (a – b)⁴= a4 – 4a³b + 6a²b² – 4ab³+ b⁴
• a⁴ – b⁴= (a – b)(a + b)(a² + b²)
• a⁵ – b⁵= (a – b)(a⁴ + a³b + a²b² + ab³+ b⁴)

Algebra Formula for Natural Numbers

Algebra formulas for Natural Numbers Except for 0 and negative numbers , the rest of the numbers [ 2 to infinity] in the number system that humans can count are known as Natural Numbrrs. Some algebraic formulas are applied when performing operations on natural numbers. They are.
Consider n to be a natural number.

1. (aⁿ – bⁿ )= (a – b)(a^n-1 + a^n-2b+…+ b^n-2a + b^n-1)
2. ( aⁿ + bⁿ)= (a + b)(a^n-1 – a^n-2b +…+ b^n-2a – b^n-1) [ where n is even  , (n = k + 1)  ]
3. (aⁿ + bⁿ )= (a + b)(a^n-1 – a^n-2b +a^n-3b²…- b^n-2a + b^n-1) [ where n is odd , (n = 2k + 1)  ]

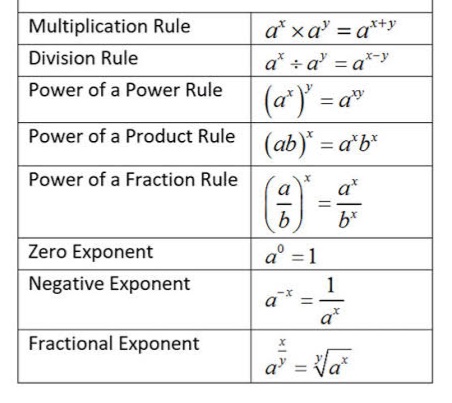
Laws of Exponents

In Algebra formulas An Exponent or power is used to demonstrate the repeated multiplication of a number. Such as 3×3×3×3 can be written as 3⁴ where 4 is the exponent of 3.   In general, exponents or powers indicate how many times a number can be multiplied. There are various rules to operate an exponent for addition, subtraction, and multiplication which are easily solved by algebraic formulas.

Algebra Formulas for Quadric equations

Algebra formulas for Quadric equations are one of the most important topics in the syllabus of Class 9 and 10 . To find the root of the given  quadric equations we used the following formulas

If ax²+bx+c =0 is a quadric equation ,then

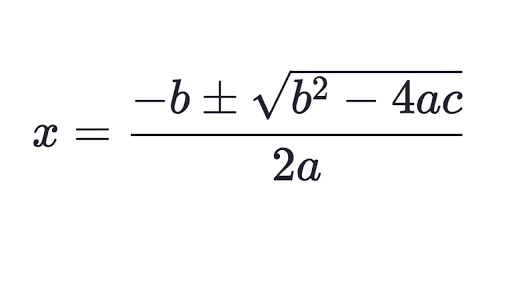
From the above formula we can conclude that , If the roots of the quadric equation are α and β
1. The equation will be (x − α)(x − β) = 0,
2.  The value of (α + β ) = (-b / a) and α × β = (c / a).

Algebra Formulas For Irrational Numbers (SSC CGL)

The formulas used to solve equations based on Irrational Numbers are following

1. √ab = √a √b
2. √a/b =√a / √b
3. ( √a +√b )  ( √a – √b ) = a-b
4. ( √a +√b )²= a + 2 √ab + b
5. ( a +√b )( a -√b )= a² – b

Algebra Formulas List

Here a list of all important Algebraic formulas is provided. Students must go through the list to solve difficult algebraic equations very quickly.

Algerbra Formula Chart

Algerbra Formula Chart is Given Below, Check Now.

a+b+c Whole Square Formula- (a+b+c)^2 Formula

The square of the sum of three terms, $a+b+c$, can be expanded using the formula for the square of a trinomial:

(a+b+c)2=a2+b2+c2+2ab+2ac+2bc

So, (a+b+c)2 is equal to the sum of the squares of the individual terms (a2, b2, c2) and twice the products of the pairs of terms ($2ab$, $2ac$, $2bc$).

This expansion holds true for any values of $a$, $b$, and $c$.

a-b Whole Square

The square of the difference between two terms, $a-b$, can be expanded using the formula for the square of a binomial:

(a−b)2=a2−2ab+b2

So, (a−b)2 is equal to the square of the first term (a2), minus twice the product of the two terms ($2ab$), and the square of the second term (b2).

This expansion holds true for any values of $a$ and $b$.

a+b Whole Square

The square of the sum of two terms, $a+b$, can be expanded using the formula for the square of a binomial:

(a+b)2=a2+2ab+b2

So, (a+b)2 is equal to the sum of the squares of the individual terms (a2 and b2) and twice the product of the terms ($2ab$).

This expansion holds true for any values of a and $b$.

Implementation of Algebra All Formula with Examples

Example 1 : Find the value 20²- 15²
Solution: To solve the  equation ,the formula we use is
a² -b² = (a+b) (a-b)
= (20+15)(20-15)
= 35 × 5
= 175 (Answer)

Example 2 : (x-y) =2 and x²+ y² =20 then find the value of x  and y [ where x,y >0 ]
Solution: Here , x²+ y² =20
(x-y)² +2xy =20
Or, (2)²+ 2xy =20
Or, 2xy = 20-4  = 16
Or,xy = 8
Now, (x+y)²= (x-y)² +4xy = (2)² +4.8 =36
Or,x+y = ± 6
So, x+y = 6 [x,y >0 ] ….(1)
We also get , x- y =2 ……(2)
Solving two equations we get ,
x = 4 and y = 2 (Answer)

Example 3 : Divide( a³ + b³ + c³ – 3abc )by( a+b+c )and the quotient.Determine the magnitude.

Solution: a+b³ + c3 – 3abc

=(a+b+c)(a²+b²+c2-ab-ac-bc)

Determinant quotient =
[(a+b+c)(a²+b²+c²-ab-ac-bc)] ÷ (a+b+c)

= a²+b²+c²-ab-be-ca.

Magnitude of quotient is  2. (Answer)

Example 4
Find their successive product (x + y), (x – y),  (x² + y²).

Solution :Determinant serial product =
(x + y) (x – y) (x² + y²)
= (x²-y²)(x² + y²)
= (x²)² – (y²)²
= x⁴ – y ⁴.( Answer)

Some Questions of Algebra Formula

1. If x+y = 3 and xy = 2, what is the value of (x – y) ² ?
2. If a+b = 8 and ab = 15, what will be the values ​​of a and b?
3. If a+b = 5 and ab = 6, Find the value of a² – b² ?
4. If x = 29 and y = 14, what is the value of (4x² + 9y²+ 12xy )?

All Algebraic Identities

Algebraic identities are equations that are true for all values of the variables involved. Here are some of the most important algebraic identities:

1. Basic Algebraic Identities

• Square of a Sum:
  $(a + b)^2 = a^2 + 2ab + b^2$

• Square of a Difference:
  $(a – b)^2 = a^2 – 2ab + b^2$

• Product of a Sum and Difference:
  $(a + b)(a – b) = a^2 – b^2$

• Cubic of a Sum:
  $(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$

• Cubic of a Difference:
  $(a – b)^3 = a^3 – 3a^2b + 3ab^2 – b^3$

• Sum of Cubes:
  $a^3 + b^3 = (a + b)(a^2 – ab + b^2)$

• Difference of Cubes:
  $a^3 – b^3 = (a – b)(a^2 + ab + b^2)$

2. Multinomial Algebraic Identities

• Square of a Trinomial:
  $(a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca$

• Cubic of a Trinomial:
  $(a + b + c)^3 = a^3 + b^3 + c^3 + 3(a + b)(b + c)(c + a)$

3. Special Algebraic Identities

• General Binomial Theorem:
  $(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k}b^k$

• (a + b + c)² Expanded:
  $(a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca$

• Sum of Powers of Roots:
  $a^n – b^n = (a – b)(a^{n-1} + a^{n-2}b + \cdots + b^{n-1})$

4. Quadratic Algebraic Identities

• For any quadratic polynomial:
  $ax^2 + bx + c = a(x – \alpha)(x – \beta)$

   where

  $\alpha$

  and

  $\beta$

  are the roots of the equation

  $ax^2 + bx + c = 0$

  .

5. Important Algebraic Products

• Sum of squares of two numbers:
  $a^2 + b^2 = \frac{(a + b)^2 + (a – b)^2}{2}$

  ​

• Product of four numbers:
  $(a^2 + b^2)(c^2 + d^2) = (ac + bd)^2 + (ad – bc)^2$

6. Miscellaneous Algebraic Identities

• Lagrange’s Identity:
  $(a^2 + b^2)(c^2 + d^2) = (ac + bd)^2 + (ad – bc)^2$

• Expression for
  $(a + b + c)^3$

  :

  $(a + b + c)^3 = a^3 + b^3 + c^3 + 3(a + b)(b + c)(c + a)$

These identities are useful in simplifying expressions, solving equations, and performing algebraic manipulations.

Algebraic Identities Formulas in Hindi

यहां कुछ बीजगणित सूत्र दिए गए हैं जिनमें वर्ग शामिल हैं।
• a²– b² = (a – b)(a + b)
• (a + b)²=  a²+ 2ab + b²
• a²+ b²= (a + b)²– 2ab
• (ए – बी)² = ए²– 2ab+ बी²
• (a + b + c)² = a² + b² + c²+ 2ab + 2bc + 2ca
• (ए – बी – सी)² = ए²+ बी²+ सी²-2ab + 2bc – 2ca

एसएससी सीजीएल के लिए बीजगणित सूत्र

यहाँ कुछ बीजगणित सूत्र दिए गए हैं जिनमें घन शामिल हैं।

• (a + b)³ = a³+ 3a²b + 3ab²+ b³
•  (a + b)³ = a³ + b³ + 3ab(a + b)
• (a – b)³= a³ – 3a²b + 3ab² – b³
• (a – b)³= a³ – b³ – 3ab(a – b)
• a³ – b³ = (a – b)(a²+ ab + b²)
• a³ + b³ = (a + b)(a²– ab + b²)

कुछ और बीजगणित सूत्र हैं –
• (a + b)⁴= a⁴+ 4a³b + 6a²b² + 4ab³ + b²
• (a – b)⁴= a4 – 4a³b + 6a²b² – 4ab³+ b⁴
• a⁴ – b⁴= (a – b)(a + b)(a² + b²)
• a⁵ – b⁵= (a – b)(a⁴ + a³b + a²b² + ab³+ b⁴)

Algebraic Formulas PDF

Check Out The Algebraic Formulas PDF for Class 10 Students. Click Here- Math Algebra Formulas PDF

Related Post:

Sharing is caring!