Area of a Circle Formula with Radius, Diameter

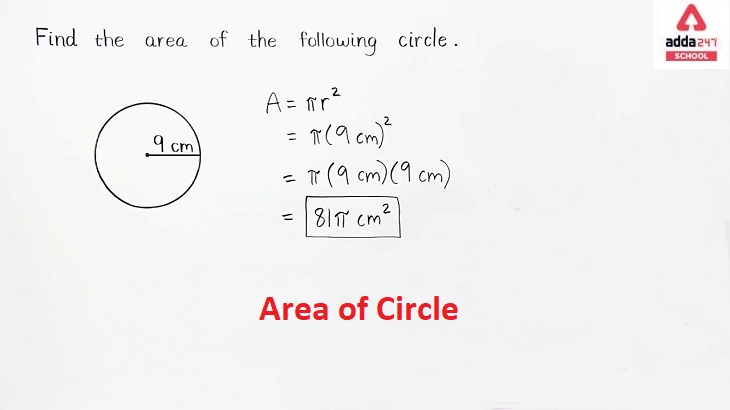
Area of Circle

To find the Area of a Circle, you simply square the radius and multiply it by π. So, if you have the radius of the circle, you can use this formula to calculate its area.

Area of a Circle Formula

The area (A) of a circle can be calculated using the formula:

Area of Circle Formula A = πr²

Where:

• A is the area of the circle,
• π (pi) is a mathematical constant approximately equal to 3.14159,
• r is the radius of the circle.

Area of a Circle

Finding Area of  Circle is very important for every student. In mathematics, a circle is a set of points in a plane that are all the same distance from a central point. Coins, dinner plates, pizza, and other items are only a few examples of circles in the real world. Radius is the distance between the center and the points. The diameter is half of the radius of the circle.  The circle is a closed 2D object made up of equidistant points around a central point. The term “circle” comes from the Greek word “kirkos,” which means “ring.”  In this article, we have discussed the properties of a circle, the definition of a circle, and the Area of Circle. 

Circle Area Formula

A circle is a locus of a point moving around a fixed point at a fixed distance away from the point. A circle is a closed curve with an exterior line equidistant from the center(Interior fixed point). The radius of the circle is the fixed distance from the fixed point(also called the center of the circle). Many examples of the circle area formula can be found in everyday life, such as the sun, ball, round playground, and so on. 

Radius formula

radius formula= diameter/2

Radius of the circle: A radius is a distance between the circle’s center and any point on it. when two radii are placed on top of each other, the resultant has the same length as one diameter. As a result, one diameter is twice the radius.

Chord: The chord is a segment of a line that joins two points on a curve. The use of a chord in geometry is focused on describing a line segment connecting two endpoints that rest on a circle.

Three Ways to Find the Area of a Circle

Calculating the area of a circle based on given information is a popular problem in geometry class. The basic formula to calculate the area of the circle is A = π2, where r is the radius of the circle. This formula we have been using since school. Here we have given the three methods to calculate the area of the circle. 

Area of a Circle with Radius

The radius of a circle is the distance between its center and its periphery. The radius will be the same regardless of which way you measure it. A circle’s radius is also twice its diameter. In most cases, you will be given a radius. If the center of the circle is not marked then it will be difficult to find the radius of the circle. 

Let us assume that the radius of the circle is 14 cm

A = πr2

Use this formula to find the area of the circle, we have given that the radius of the circle is 14 cm. And we know that the value of π is 22/7 put these values is in the given formula to calculate the area of the circle. 

A = 22/7*14*14

A= 616 Cm2

Area of a Circle with a Diameter

If the diameter is given then it’s easy to calculate the area of the circle. We have learned that the diameter is twice the radius, if the radius is given then it’s easy to find the area of the circle. 

A = πr2

We can put  radius = 2* diameter

A = π(2d)2

Example: Assume that the diameter of the circle is 28cm, then find the area of the circle.

Solution: We know that the value of π is 22/7 and it’s unitless, and we have given the diameter of a circle which is 28cm.

A = 22/7(2*28)2

A = 9856 cm2

We have got the area of the circle which is A = 9856 cm2

Area of a circle with Circumference

Here we have given the method to calculate the area of the circle using the circumference of the circle. If the radius of a circle and diameter of the circle is not given and only circumference is given then we can use the formula given below to find the area of the circle.

A = C2/4π

Example: Assume the circumference of the circle is 7cm

Solution: We have given the circumference of the circle, so we will use the formula given above to find the area of the circle. 

A = C2/4π

A = 7*7/4*(22/7)

A = 3.89 cm2

We have got the area of the circle is A = 3.89 cm2

Hence, we have covered the three ways to calculate the area of the circle. The students must use all three methods to calculate the area of the circle. To ease of students we have provided the examples, students must refer to the examples and practice as much as they can. 

How to Find the Area of a Circle in Hindi

वृत्त के क्षेत्रफल की गणना करना ज्यामिति वर्ग में एक लोकप्रिय समस्या है। वृत्त के क्षेत्रफल की गणना करने का मूल सूत्र A = 2 है, जहाँ r वृत्त की त्रिज्या है। यह फॉर्मूला हम स्कूल से इस्तेमाल कर रहे हैं। यहाँ हमने वृत्त के क्षेत्रफल की गणना करने की तीन विधियाँ दी हैं।

त्रिज्या के साथ वृत्त का क्षेत्रफल

एक वृत्त की त्रिज्या उसके केंद्र और उसकी परिधि के बीच की दूरी है। त्रिज्या वही होगी, चाहे आप इसे किसी भी तरह से मापें। एक वृत्त की त्रिज्या भी उसके व्यास की दुगुनी होती है। ज्यादातर मामलों में, आपको एक दायरा दिया जाएगा। यदि वृत्त का केंद्र अंकित नहीं है तो वृत्त की त्रिज्या ज्ञात करना कठिन होगा।

मान लीजिए कि वृत्त की त्रिज्या 14 सेमी . है

ए = r2

वृत्त का क्षेत्रफल ज्ञात करने के लिए इस सूत्र का प्रयोग करें, हमने दिया है कि वृत्त की त्रिज्या 14 सेमी है। और हम जानते हैं कि का मान 22/7 है, इन मानों को वृत्त के क्षेत्रफल की गणना करने के लिए दिए गए सूत्र में है।

ए = 22/7*14*14

ए = 616 सेमी2

व्यास के साथ वृत्त का क्षेत्रफल

यदि व्यास दिया गया हो तो वृत्त का क्षेत्रफल निकालना आसान हो जाता है। हमने सीखा है कि व्यास त्रिज्या का दोगुना है, यदि त्रिज्या दी गई है तो वृत्त का क्षेत्रफल ज्ञात करना आसान है।

ए = r2

हम डाल सकते हैं त्रिज्या = 2* व्यास

ए = π(2डी)2

उदाहरण: मान लीजिए कि वृत्त का व्यास 28 सेमी है, तो वृत्त का क्षेत्रफल ज्ञात कीजिए।

हल: हम जानते हैं कि का मान 22/7 है और यह इकाई रहित है, और हमने एक वृत्त का व्यास दिया है जो कि 28 सेमी है।

ए = 22/7(2*28)2

ए = 9856 सेमी2

हमें वृत्त का क्षेत्रफल मिला है जो A = 9856 cm2 . है

परिधि वाले वृत्त का क्षेत्रफल

यहां हमने वृत्त की परिधि का उपयोग करके वृत्त के क्षेत्रफल की गणना करने की विधि दी है। यदि किसी वृत्त की त्रिज्या और वृत्त का व्यास नहीं दिया गया है और केवल परिधि दी गई है तो हम वृत्त का क्षेत्रफल ज्ञात करने के लिए नीचे दिए गए सूत्र का उपयोग कर सकते हैं।

ए = सी2/4π

उदाहरण: मान लें कि वृत्त की परिधि 7cm . है

हल: हमने वृत्त की परिधि दी है, इसलिए हम वृत्त का क्षेत्रफल ज्ञात करने के लिए ऊपर दिए गए सूत्र का उपयोग करेंगे।

ए = सी2/4π

ए = 7*7/4*(22/7)

ए = 3.89 सेमी2

हमें वृत्त का क्षेत्रफल A = 3.89 cm2 . मिला है

इसलिए, हमने वृत्त के क्षेत्रफल की गणना करने के तीन तरीकों को शामिल किया है। विद्यार्थियों को वृत्त के क्षेत्रफल की गणना करने के लिए तीनों विधियों का उपयोग करना चाहिए। छात्रों की सुविधा के लिए हमने उदाहरण प्रदान किए हैं, छात्रों को उदाहरणों का उल्लेख करना चाहिए और जितना हो सके अभ्यास करना चाहिए।

Sharing is caring!