Area of Rhombus Formula and Examples for Class 8

Area of rhombus can be calculated using the lengths of diagonals. Area of rhombus formula to find area in this case is given as: Area = (d1 × d2)/2 sq. units.

Rhombus is a parallelogram that has opposite sides parallel to each other and the opposite angles are also equal. The adjacent sides are supplementary.

Area of Rhombus

All the sides of a rhombus are equal, hence it is an equilateral quadrilateral. The diagonals are also bisectors of each other.

It is different from the square because, a square and rhombus both have equal sides, but all the angles in the square are right-angled and the angles in a rhombus are different.

The area of a rhombus can be calculated using different methods, but one of the common approaches is to use the formula:

Area = (diagonal1 × diagonal2) / 2

Where:

“diagonal1” and “diagonal2” are the lengths of the two diagonals of the rhombus that intersect at a 90-degree angle.

This formula is derived from the fact that a rhombus can be split into four congruent right-angled triangles. The product of the lengths of the diagonals divided by 2 gives the area of each triangle, and since there are four triangles, the total area of the rhombus is the sum of their areas.

Remember that the diagonals are the line segments connecting opposite vertices of the rhombus, and they intersect at a 90-degree angle. Make sure to use the correct lengths for the diagonals when applying the formula.

Rhombus Area Formula

Some Different formulas to find the area of rhombus are:

Formulas to Calculate Area of Rhombus
Using Diagonals	A = ½ × d₁ × d₂
Using Base and Height	A = b × h
Using Trigonometry	A = b² × Sin(a)

Where, The value of d_{1 and}d_{2 are}

d₁= length of diagonal 1
d₂= length of diagonal 2
b = length of any side
h = height of rhombus
a = measure of any interior angle

Formulas to find the Area of a Rhombus

By using the base and height formula

In the base and height formula, the base and the height of the rhombus are given, it is similar to finding the area of a parallelogram.

Steps to find the area of a rhombus with base and height.

-find the base and the height of the rhombus, the base will be any side of the rhombus and the height will be the perpendicular line joining the diagonal and the base.

– Base X Height = Area of the rhombus.

Example-

Find the area of a rhombus with base, 5cm, and height, 4cm?

Area of Rhombus = Base X Height

Area of rhombus = 5cm X 4cm

20 cm square = area of the Rhombus.

By using Diagonals

Before getting into the formula, let’s know how we get the formula of calculating the area of Rhombus by using the diagonals.

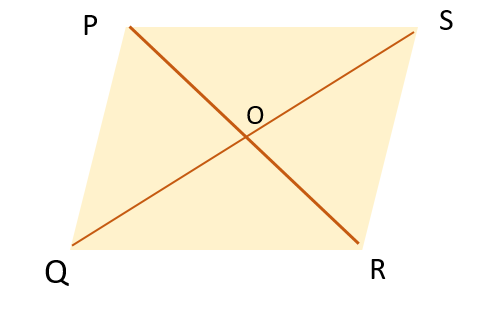
Given

Let PQRS be a rhombus
O is the intersection point
All the four sides are congruent to each other
All the angles are opposite and equal.

The area of rhombus PQRS = Area of triangle PQS and area of triangle QRS.

2 X Area of PQS (Triangle PQS and triangle QRS are congruent)

Now,

Area of Triangle PQS = ½ x base X-height

= ½ x QS x PQ —————- (1)

= ½ x QS X ½ X PQ

= ¼ (QS X PR), (Because PQ = PR/2)—————–(2)

From equation (1) and (2)

Area of rhombus = area of triangle PQS

2 x ¼ x QS X PR = ½ X QS X PR

1/2 X QS (Diagonal 1) X PR (Diagonal 2)

Example-

Find the area of a rhombus diagonal 1 measuring 6cm and diagonal 2, measuring 8cm?

Diagonal 1 = 6cm—- D1

Diagonal 2 = 8cm—- D2

Area of the rhombus = ½ x D1 and D2

½ x 6cm x 8cm = ½ x 48 = 24 cm square.

Therefore, the area of the rhombus is 24 cm square.

Word meanings used for Area of Rhombus Formulas and Definition

Parallelogram- A four-sided polygon with opposite sides equal.
supplementary- Two angles are supplementary if their sum is 180 degrees.
Bisect- Divided into two parts
Adjacent- next to each other
Congruent- same angle and same sides of two triangles make them congruent.

Area of Rhombus Example Questions

Find the area of a chocolate box-shaped in the form of a rhombus with diagonals measuring 12 cm and 16 cm.
D1= 12cm

D2= 16cm

Area of the chocolate box = ½ x D1x D2

½ x 12 x 16 = ½ x 192 = 96 cm square.

Hence, the area of the chocolate box is 96 cm square.

Asha owns a shoe rack, she shifted to a new house and is trying to place everything accordingly. She wants to know the area of the shoe rack so that she can place it well. What is the area of the shoe rack with a base of 45cm and height of 60 cm?
Given,

Base = 45 cm

Height = 60 cm

Area of the shoe rack = base x height

45cm x 60 cm = 2700 cm square

Hence, the area of the shoe rack is 2700 cm square.

FAQs

How to find the area of the rhombus if the measurement of only one diagonal is given?

If only one measurement is given, to find the second one use Pythagoras theory with the help of the measurement of the sides.

Perimeter and area of a rhombus are the same?

No, both are different. The perimeter of rhombus = 4a, where a is the side and area of the rhombus = base x height or ½ x diagonal1 and diagonal 2.

Can we use trigonometry to find the area of the rhombus?

Yes, it is an alternative formula to find the area of the rhombus.
Area = square of the sides x sin (a), where a is an interior angle.

Rhombus and square are the same?

No, rhombus, and square are two different geometric shapes, the square has all the sides the same with all the angles forming right-angle, whereas in rhombus the sides are equal but the angles are different.