Arithmetic Progression, Definition, Nth Term, Formulas, Sum, Solved Examples, PYQ PDF

Table of Contents

An arithmetic progression (AP) is a list or sequence of numbers in which each term is obtained by adding a fixed number “d” to the preceding term, except the first term a. The fixed number or the added number “d” is called this series’s common difference. For example, the natural number sequence 1, 2, 3, 4, 5, 6,7, 8, 9… is an Arithmetic Progression (AP) with a common difference of 1 (difference between every two numbers), 1 is presenting “d” in this sequence. Even with odd and even numbers, the common difference between two consecutive terms is equal to 2. We will look at the concept of arithmetic progression in this article, the AP formulas for determining the nth term, common difference, and sum of n terms. We will solve a variety of examples with detailed answers based on the arithmetic progression formula and PYQ pdf to gain a better understanding of the topic.

Arithmetic Progression

Arithmetic progression is available in our daily lives. For example, the number of days in a week, or months in a year, or the salary hikes in employees. Mathematicians have generalized this pattern of series (AP) and sequences into progressions.

Definition

Arithmetic progression (AP) is a numerical sequence in which the difference between any two subsequent numbers is a constant value. AP is also known as the “Arithmetic Sequence”. A real-life example of an AP is the sequence produced by a student’s school fees, which increases by a fixed sum of 2000 rupees each year.

Arithmetic Progression Formulas

Arithmetic progression can be expressed in a general form. there are also two very important formulas of AP that you will use to solve questions –

nth Term of AP Formula
The sum of all N terms of an AP

General Structure of AP

The general form of an AP is 𝑎, 𝑎 + 𝑑, 𝑎 + 2𝑑, 𝑎 + 3𝑑, . …
In the list of numbers 𝑎1 , 𝑎2 , 𝑎3 ,… if the differences 𝑎2 – 𝑎1 , 𝑎3 – 𝑎2 , 𝑎4 – 𝑎3 , . .. give the same value, i.e., if 𝑎𝑘+1 – 𝑎𝑘 is the same for different values of k, then the given list of numbers is an AP.

Arithmetic Progression nth Term

The nth term an (or the general term) of an AP is 𝑎𝑛 = 𝑎 + (𝑛– 1)𝑑, where a is the first term
and d is the common difference. Note that 𝑎1 = 𝑎.

Sum of N Terms of Arithmetic Progression (AP)

The sum 𝑆𝑛 of the first n terms of an AP is given by 𝑆𝑛 = 𝑛/2 [2𝑎 + (𝑛 − 1)𝑑]
If 𝑙 is the last term of an Arithmetic Progression (AP) of “n” terms, then the sum of all the terms can also be given by
𝑆𝑛 = 𝑛/2 [𝑎 + 1]
Sometimes 𝑆𝑛 is also denoted by S.
If 𝑆𝑛 is the sum of the first n terms of an AP, then its 𝑛𝑡ℎ term 𝑎𝑛 is given by 𝑎𝑛 = 𝑆𝑛 – 𝑆𝑛−1

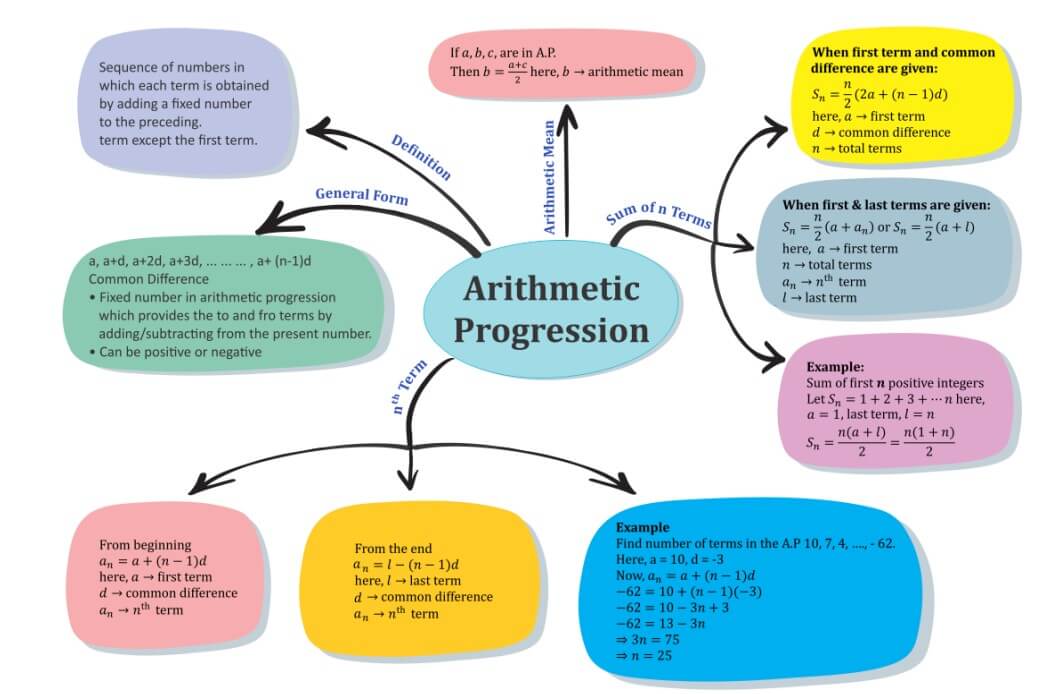
AP Formulas List in Flowchart

Students can revise the full concepts of ap anf the important formulas from this flowchart.

Arithmetic Progression Examples with Solutions

Practice this 10 questions with solutions to practoice the ap formulas –

Q1. Write the nth term of the A.P. 1/𝑚 , 1+𝑚/𝑚, 1+2𝑚/𝑚, ….
Sol. Given AP is
1/𝑚 ,1+𝑚/𝑚, 1+2𝑚/𝑚, … … … …
We have,
𝑎 =1/𝑚
Now, 𝑑 =1+𝑚/𝑚 − 1/𝑚 = 1+𝑚−1/𝑚 = 1
We know that
𝑎_𝑛 = 𝑎 + (𝑛 − 1)𝑑
∴ 𝑎_𝑛 =1/𝑚 + (𝑛 − 1)1 =/1𝑚 + 𝑛 − 1
Hence, 𝑎_𝑛 = 1+(𝑛−1)𝑚/𝑚

Q2. For what value of k will 𝑘 + 9, 2𝑘 − 1 and 2𝑘 + 7 are the consecutive terms of an A.P.?
Sol. We have
Consecutive terms of an AP are
k + 9, 2k – 1, 2k + 7
Then,
⇒ (𝑘 + 9) + (2𝑘 + 7) = 2(2𝑘 − 1)
{since if 𝑎, 𝑏, 𝑐 are in AP, then 𝑎 + 𝑐 = 2𝑏}
⇒ 𝑘 + 9 + 2𝑘 + 7 = 4𝑘 − 2
⇒ 3𝑘 + 16 = 4𝑘 − 2
⇒ 16 + 2 = 4𝑘 − 3𝑘
⇒ 𝑘 = 18

Q3. If 𝑆𝑛, the sum of first 𝑛 terms of an A.P. is given by 𝑆𝑛 = 3𝑛
2 − 4𝑛. Find the 𝑛𝑡ℎ term.
Sol. Given
𝑆𝑛 = 3𝑛
2 − 4𝑛
We have
𝑎1 = 𝑆1 = 3(1)
2 − 4(1) = 3 − 4 = −1
𝑎2 = 𝑆2 − 𝑆1
= [3(2)
2 − 4(2)] − (−1) = 12 − 8 + 1 = 5
∴ 𝑑 = 𝑎2 − 𝑎1 = 5 − (−1) = 6
Hence,
𝑎𝑛 = −1 + (𝑛 − 1) × 6 = 6𝑛 − 7

Q4. The sum of the first 7 terms of an A.P. is 63 and that of its next 7 terms is 161. Find the A.P.
Sol. Given
𝑆₇ = 63
We have,
𝑆_𝑛 =𝑛/2[2𝑎 + (𝑛 − 1)𝑑]
So,
𝑆₇ =7/2[2𝑎 + 6𝑑] = 63
Or
2𝑎 + 6𝑑 = 18 … (i)
Now, sum of 14 terms is:
𝑆₁₄ = 𝑆𝑓𝑖𝑟𝑠𝑡 7 𝑡𝑒𝑟𝑚𝑠 + 𝑆𝑛𝑒𝑥𝑡 7 𝑡𝑒𝑟𝑚𝑠 = 63 + 161 = 224
∴14/2 [2𝑎 + 13𝑑] = 224
⇒ 2𝑎 + 13𝑑 = 32 … (ii)
On subtracting (i) from (ii), we get
(2𝑎 + 13𝑑) − (2𝑎 + 6𝑑) = 32 − 18
⇒ 7d = 14
⇒ d = 2
Putting the value of d in (“i”equation), we get
2𝑎 + 6(2) = 18
2𝑎 = 18 − 12
a = 3
Hence, the A.P. will be: 3, 5, 7, 9, … ………..

Q5. Show that (𝑎 − 𝑏)², (𝑎² + 𝑏²) and (𝑎 + 𝑏)² are in A.P.

Sol. Given
(𝑎 − 𝑏)², (𝑎² + 𝑏²) and (𝑎 + 𝑏)²
Common difference,
𝑑₁ = (𝑎² + 𝑏²) − (𝑎 − 𝑏)² = 𝑎² + 𝑏² − (𝑎² + 𝑏² − 2𝑎𝑏)
= 𝑎² + 𝑏² − 𝑎² − 𝑏² + 2𝑎𝑏 = 2𝑎𝑏
and 𝑑₂ = (𝑎 + 𝑏)² − (𝑎² + 𝑏²)
= 𝑎² + 𝑏² + +2𝑎𝑏 − 𝑎² − 𝑏²
= 2𝑎𝑏
Since, 𝑑₁ = 𝑑₂
Hence, (𝑎 − 𝑏)², (𝑎² + 𝑏²) and (𝑎 + 𝑏)² are in A.P.

Q6. How many terms of the A.P. −6, −11/2, −5, -9/2…….. are needed to give their sum zero.

Sol. Given 𝑎 = −6 𝑎𝑛𝑑 𝑑 = − 11 − (−6) = 1
Since, 𝑆_𝑛= 𝑛/2 [2𝑎 + (𝑛 − 1)𝑑]
Let sum of 𝑛 terms be zero.
∴ 𝑆_𝑛 = 0
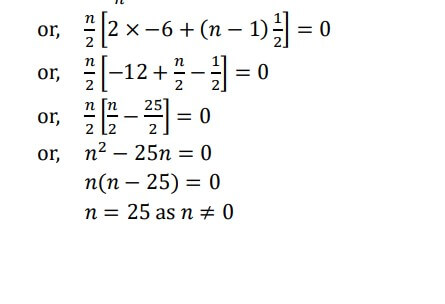Hence, required terms are 25.

Q7. In a certain A.P. 32th term is twice the 12th term. Prove that 70th term is twice the 31st term.
Sol. Let the 1st term be a and common difference be ‘d’.
According to the question, 𝑎32 = 2𝑎12
∴ 𝑎 + 31𝑑 = 2(𝑎 + 11𝑑)
𝑎 + 31𝑑 = 2𝑎 + 22𝑑
𝑎 = 9𝑑
Again, 𝑎₇₀ = 𝑎 + 69𝑑
= 9𝑑 + 69𝑑 = 78𝑑
∵ 𝑎₃₁ = 𝑎 + 30𝑑
= 9𝑑 + 3𝑑 = 39𝑑
Hence, 𝑎₇₀ = 2𝑎₃₁
Hence Proved.

Q8. The 8th term of an A.P. is zero. Prove that its 38th term is triple of its 18th term.
Sol. Given, 𝑎₈ = 0 or, 𝑎 + 7𝑑 = 0 or, 𝑎 = −7𝑑
or, 𝑎₃₈ = 𝑎 + 37𝑑
or, 𝑎₃₈ = −7𝑑 + 37𝑑 = 30𝑑
And, 𝑎₁₈ = 𝑎 + 17𝑑
= −7𝑑 + 17𝑑 = 10𝑑
or, 𝑎₃₈ = 30𝑑 = 3 × 10𝑑 = 3 × 𝑎18
∴ 𝑎₃₈ = 3𝑎₁₈.
Hence Proved.

Q9. Show that the sum of all terms of an A.P. whose first term is a, the second term is b and the last term is c is equal to (𝑎+𝑐)(𝑏+𝑐−2𝑎).
2(𝑏−𝑎)
Sol. Given, first term, A = a and second term = b
⇒ common difference, d = b − a
Last term, 𝑙 = 𝑐

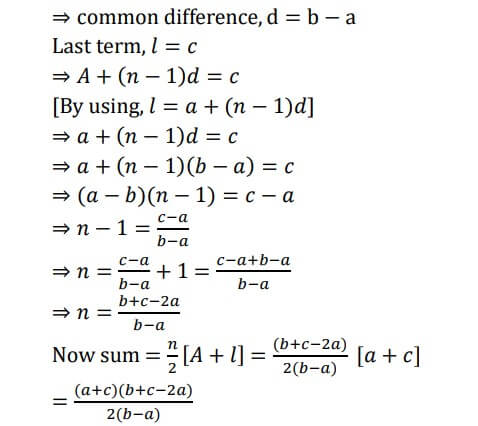
Q10. For what value of n, are the 𝑛𝑡ℎ terms of two A.Ps 63, 65, 67, … and 3, 10, 17, … equal?
Sol. Let a, d and A, D be the 1st term and common different of the 2 A.P.s respectively.
Here,
𝑎 = 63, 𝑑 = 2
A = 3, D = 7
Given, 𝐴𝑛 = 𝐴𝑛
⇒ 𝑎 + (𝑛 − 1)𝑑 = 𝐴 + (𝑛 − 1)𝐷
⇒ 63 + (𝑛 − 1)2 = 3 + (𝑛 − 1)7
⇒ 63 + 2𝑛 − 2 = 3 + 7𝑛 − 7
⇒ 61 + 2𝑛 = 7𝑛 − 4
⇒ 5𝑛 = 65
⇒ 𝑛 = 13

Download more Solved questions with answers – Most Repeated PYQ of AP (Arithmetic Progression)

Arithmetic Progression PDF

Students generally search for all practice questions for the arithmetic progression chapter. So our Math team has compiled all the important AP-related questions, even all previous year questions that have come to class 10 and other exams in a single pdf. Download all the pdf from the below-given link and start solving.