BODMAS rule stands for the bracket, order, division, multiplication, addition, and subtraction. It is used to solve mathematical expression that consists of complex equations including addition, subtraction, multiplication, division, bracket, and order. Check BODMAS Full form and Rules in Mathematics
BODMAS
BODMAS gives the right order to solve mathematical equations without missing any step. According to the BODMAS rule, to solve any equation, we should first evaluate the brackets and solve anything inside them. After bracket, evaluate the powers, roots, or exponents. All the calculations are done from left to right. Then evaluate the equation for division and multiplication and then followed by addition and subtraction. Here, addition and subtraction are of the same priority, so, you can choose to do addition first or subtraction first. The same goes with multiplication and division, you can which one to do first.
BODMAS Full Form in Mathematics
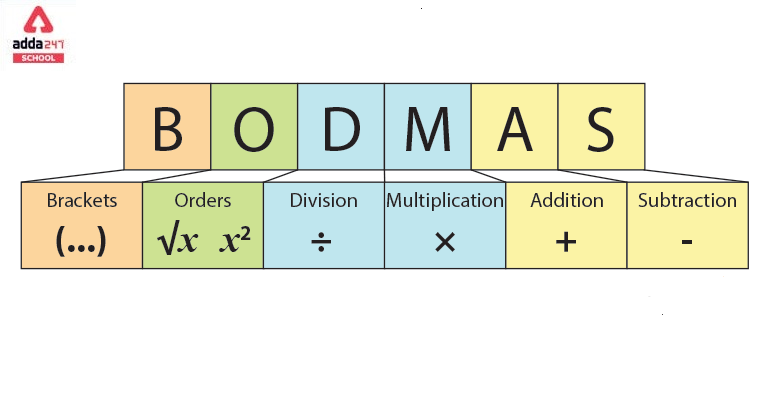
BODMAS stands for: Brackets, Orders (powers and square roots, etc.), Division, Multiplication, Addition, Subtraction
It is a rule used to determine the correct sequence in which operations are to be performed in a mathematical expression.
BODMAS consists of the first letter of the operations involved in a mathematical equation.
B- Bracket (), [], {}
O- Order, Square root, exponents, and powers
D- Division, ÷ /
M- Multiplication × *
A – Addition +
S – Subtraction –
Here, we can see there are three types of brackets, how will you decide, which bracket to solve first? Brackets within brackets are very complex equations, different bracket implies different part of the equation.
| Bracket | Name |
| ( ) | Parentheses |
| [] | Brackets or square brackets |
| { } | Braces or Curly bracket |
Parentheses are the innermost bracket in any equation, followed by braces and square brackets. Carry out the required operations in the parentheses first, then with basic mathematical calculation remove the brackets. If there is no sign between the brackets, it implies multiplication. Similarly, evaluate the braces and the square brackets.
BODMAS Rule
The BODMAS rule, is a mathematical acronym used to clarify the order of operations in mathematical expressions. It stands for:
B – Brackets (or Parentheses) O – Orders (or Exponents and Powers) D – Division M – Multiplication A – Addition S – Subtraction
The BODMAS rule helps ensure that mathematical expressions are evaluated correctly by establishing a specific order in which operations should be performed.
Here’s a breakdown of each component of the BODMAS rule:
- Brackets (or Parentheses): Any operations enclosed within brackets should be performed first. This includes evaluating expressions inside parentheses (), square brackets [], or curly braces {}.
For example: (2 + 3) × 4 = 5 × 4 = 20
- Orders (or Exponents and Powers): Evaluate any exponents or powers (numbers raised to a certain power) next.
For example: 2^3 = 2 × 2 × 2 = 8
- Division: Perform any divisions from left to right.
For example: 10 ÷ 2 ÷ 5 = 5 ÷ 5 = 1
- Multiplication: Perform any multiplications from left to right.
For example: 2 × 3 × 4 = 6 × 4 = 24
- Addition: Perform any additions from left to right.
For example: 2 + 3 + 4 = 5 + 4 = 9
- Subtraction: Perform any subtractions from left to right.
For Example: 10 – 3 – 2 = 7 – 2 = 5
By following the BODMAS rule, mathematicians and students can ensure that mathematical expressions are evaluated in a consistent and correct manner. It helps to avoid ambiguity and ensures that everyone obtains the same result when solving mathematical problems.
BODMAS Full Form in Computer
BODMAS rule was invented by Archillies Resefelt. He was a mathematician. He made it into a mnemonic that can be remembered easily, he made the First Letter of the operation into a word so that we can remember it and carry out calculations easily. The BODMAS rule determines the order of the equation.
Concept of BODMAS
In any mathematical expression or any equation, there are two components, numbers, and operations.
Numbers – A number is a mathematical component or value which represents the quantity and it is generally used for counting and calculations. Numerals are the symbols that represent numbers.
These are classifications of numbers
- natural numbers
- irrational numbers
- rational number
- real numbers
- whole numbers
- integers
- complex numbers
Operations- those are the characters that combine numbers and form equation
These operations are used in mathematics
- addition
- subtraction
- division
- multiplication
These numbers and operations make complex equations which also includes fraction and orders, to solve these equations we need to follow the correct steps to find the correct answer. With the use of BODMAS, we can calculate the correct answer with the correct sequence.
VBODMAS Full Form
VBODMAS stands for:
V: Vinculum (or Bar)
B: Brackets
O: Order (powers and roots, also known as indices)
D: Division
M: Multiplication
A: Addition
S: Subtraction
It represents the order of operations used to solve mathematical expressions. The vinculum (or bar) is used to indicate that the operations beneath it should be performed first, followed by the sequence of brackets, orders, division, multiplication, addition, and subtraction.
BODMAS ka Full Form in Hindi
बोडमास नियम का आविष्कार आर्चिलीज रेसेफेल्ट ने किया था। वह एक गणितज्ञ थे। उन्होंने इसे एक स्मृतिचिह्न बनाया जिसे आसानी से याद किया जा सकता है, उन्होंने ऑपरेशन के पहले अक्षर को एक शब्द में बनाया ताकि हम इसे याद रख सकें और गणना आसानी से कर सकें। BODMAS नियम समीकरण के क्रम को निर्धारित करता है।
बोडमास की अवधारणा
किसी भी गणितीय व्यंजक या किसी समीकरण में दो घटक, संख्याएँ और संक्रियाएँ होती हैं।
संख्याएँ – एक संख्या एक गणितीय घटक या मान है जो मात्रा का प्रतिनिधित्व करता है और इसका उपयोग आमतौर पर गिनती और गणना के लिए किया जाता है। अंक वे प्रतीक हैं जो संख्याओं का प्रतिनिधित्व करते हैं।
ये संख्याओं के वर्गीकरण हैं
प्राकृतिक संख्याएं
तर्कहीन संख्या
परिमेय संख्या
वास्तविक संख्या
पूर्ण संख्याएं
पूर्णांकों
जटिल आंकड़े
संक्रियाएँ- वे वर्ण हैं जो संख्याओं को जोड़ते हैं और समीकरण बनाते हैं
इन संक्रियाओं का उपयोग गणित में किया जाता है
योग
घटाव
विभाजन
गुणा
ये संख्याएँ और संक्रियाएँ जटिल समीकरण बनाती हैं जिनमें भिन्न और क्रम भी शामिल हैं, इन समीकरणों को हल करने के लिए हमें सही उत्तर खोजने के लिए सही चरणों का पालन करने की आवश्यकता है। बोडमास के प्रयोग से हम सही क्रम के साथ सही उत्तर की गणना कर सकते हैं।
BODMAS Questions Problems with Examples
Let’s carry out an expression step by step by using the BODMAS rule.
Question– 6 x (3 x 32) ÷ 3+5 – 6 =?
Solution –
Step 1. Brackets ()
The equation in the bracket is (3 x 32), according to the BODMAS rule, first solve the bracket.
3 × 32 – here, solve the order, which is 32
32= 9
Now, we have 3×9= 27
Therefore, the equation becomes 6×27÷ 3+5 – 6 =?
Step 2. Division and multiplication ÷ ×
Carry out both division and multiplication in the equation. Start the calculation from left to right
6×27= 162
162÷3= 54
Now, the equation we get is 54+5-6=?
Step 3. Addition and subtraction + –
Same as above follow the left to right order for calculation.
Add and subtract the equation,
54+5= 59
59-6= 53
The answer is 53.
Hence, 6 x (3 x 32) ÷ 3+5 – 6 = 53
Sample questions
Level I
- Simply:
- 12+(9+6×4)
Solution –
12+ (9+24)
= 12+ 33
= 45
- (8+4-7+3) ÷2
Solution-
= (12-10) ÷2
=2÷2
=0
- 5×3-4+6(without bracket)
Multiple first
5×3 = 15
Then addition
4+6= 10
Next, subtract,
15-10= 5
Level II
- Simply:
- 500÷ [10{(15-12) + (12-10)}]
First, Simplify {} and operate the equation inside it
= 500 ÷ [10{3+2}]
= 500÷ [10{5}]
Now, simplify []
=500÷50
= 10
- 1/4{6[(12+4) – (10+2)]}
Simply (), followed by [] and {}
=1/4{6[16-12])
= 1/4{6[4]}
=1/4{24}
= 6
Level III
- Simply
- 1/2- (6/4 of 3/6) + 1/4
1/2-(6/4 × 3/6) + 1/4
=1/2-3/4-1/4
= 12-9-6/24
= 12-3/24
=9/24= 3/8








 AILET Answer Key 2026 , Download Provisi...
AILET Answer Key 2026 , Download Provisi...
 AILET Question Paper 2026 with Solution,...
AILET Question Paper 2026 with Solution,...
 UP NEET Counselling 2025 Round 5 Merit L...
UP NEET Counselling 2025 Round 5 Merit L...














