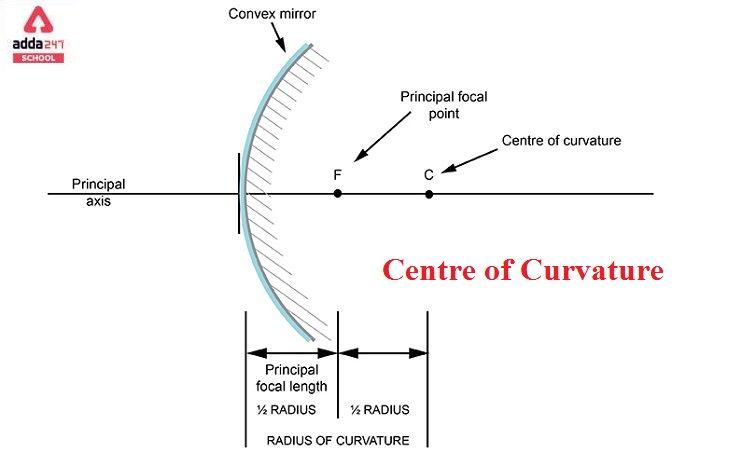
Centre of curvature: Meaning, Definition for Class 10 -

Table of Contents

Centre of Curvature: The centre of curvature refers to a point on the principal axis of a curved mirror or lens, which lies at a distance equal to the radius of curvature from the mirror or lens. It is denoted by the letter ‘C.’

In the case of a concave mirror, the center of curvature lies in front of the mirror, while for a convex mirror, it lies behind the mirror. For a converging lens, the center of curvature is located on the same side as the object, while for a diverging lens, it is on the opposite side.

The centre of curvature plays a crucial role in determining the properties of curved mirrors and lenses. For instance, when parallel rays of light strike a concave mirror, they converge at the center of curvature. Similarly, when parallel rays pass through a converging lens, they also converge at the center of curvature. This property enables the formation of real and inverted images in certain optical systems.

It’s important to note that the centre of curvature is a theoretical point, and it may not physically exist in some cases, especially with lenses or mirrors that have complex shapes. Nonetheless, the concept of the center of curvature is still applicable in analyzing and understanding the behavior of curved optical surfaces.

Centre of Curvature Meaning

The centre of curvature of a curve is determined at a position on the normal vector that is a distance from the curve equal to the radius of curvature. If the curvature is zero, it is the point at infinity. The osculating circle is located at the curve’s centre of curvature. The junction point of two infinitely close normal lines to the curve was designated by Cauchy as the centre of curvature. The evolution of the curve is made up of the locus of centres of curvature for each point on the curve.
It’s also known as the spherical distance between the point where all the rays falling on a lens or mirror appear to converge or diverge from the lens or mirror itself. Convex lenses and concave mirrors have light beams that converge, whereas concave lenses and convex mirrors have light rays that diverge.

Read About: What are Isobars?

Centre of Curvature Definition Class 10

Nicole Oresme, a philosopher and mathematician, proposes the concept of curvature as a measure of deviation from straightness in her book Tractatus de configuration bus qualitatum et motuum. He considers the centre of curvature of a circle to be inversely proportionate to the radius. He also tries to apply this concept to other curves in the form of a continually varying magnitude.
Osculating circles were used to define the curvature of a differentiable curve at first. Augustin-Louis Cauchy demonstrated that the curve’s centre of curvature is the intersection point of two infinitely close normal lines.
Curvature is a term that refers to a number of closely related geometric topics. The curvature of a curve or the curvature of a surface is the amount by which it deviates from being a straight line or a plane.
The circle, which has a curvature equal to the reciprocal of its radius, is the canonical example of a curve. Curvature is higher in smaller circles as they bend more sharply. The curvature of a differentiable curve’s osculating circle, or the circle that best approximates the curve near this point, is the curvature of the curve.
Curvature is more complicated for surfaces embedded in Euclidean space since it is dependent on the direction chosen on the surface or manifold. The terms maximal curvature, minimal curvature, and mean curvature are derived from this.
One can define the curvature intrinsically, that is, without referring to an external space, for Riemannian manifolds that are not always embedded in a Euclidean space.

Read About: Double Circulation

What is centre of curvature in Hindi?

Centre of Curvature: वक्र के वक्रता केंद्र को सामान्य वेक्टर पर एक स्थिति पर निर्धारित किया जाता है जो वक्रता की त्रिज्या के बराबर वक्र से दूरी है। यदि वक्रता शून्य है, तो यह अनंत का बिंदु है। ऑस्क्यूलेटिंग सर्कल वक्र के वक्रता केंद्र पर स्थित है। वक्र के दो असीम रूप से करीब सामान्य रेखाओं के जंक्शन बिंदु को कॉची द्वारा वक्रता के केंद्र के रूप में नामित किया गया था। वक्र का विकास वक्र पर प्रत्येक बिंदु के लिए वक्रता केंद्रों के स्थान से बना होता है। “लेंस और दर्पण” शब्द का प्रयोग आमतौर पर भौतिकी में लेंस और दर्पण के अध्ययन के संदर्भ में किया जाता है।
इसे उस बिंदु के बीच गोलाकार दूरी के रूप में भी जाना जाता है जहां लेंस या दर्पण पर पड़ने वाली सभी किरणें लेंस या दर्पण से ही अभिसरण या विचलन करती दिखाई देती हैं। उत्तल लेंस और अवतल दर्पण में प्रकाश किरणें होती हैं जो अभिसरण करती हैं, जबकि अवतल लेंस और उत्तल दर्पण में प्रकाश किरणें होती हैं जो विचलन करती हैं।

एक दार्शनिक और गणितज्ञ निकोल ओरेस्मे ने अपनी पुस्तक ट्रैक्टैटस डी कॉन्फिगरेशन बस क्वालिटैटम एट मोटुम में सीधेपन से विचलन के एक उपाय के रूप में वक्रता की अवधारणा का प्रस्ताव दिया है। वह एक वृत्त की वक्रता को त्रिज्या के व्युत्क्रमानुपाती मानता है। वह इस अवधारणा को लगातार बदलते परिमाण के रूप में अन्य वक्रों पर भी लागू करने का प्रयास करता है।
पहले अवकलनीय वक्र की वक्रता को परिभाषित करने के लिए ऑस्कुलेटिंग सर्कल का उपयोग किया गया था। ऑगस्टिन-लुई कॉची ने प्रदर्शित किया कि वक्र का वक्रता केंद्र दो असीम रूप से बंद सामान्य रेखाओं का प्रतिच्छेदन बिंदु है।
वक्रता एक ऐसा शब्द है जो कई निकट से संबंधित ज्यामितीय विषयों को संदर्भित करता है। किसी वक्र की वक्रता या सतह की वक्रता वह राशि है जिससे वह एक सीधी रेखा या समतल होने से विचलित हो जाती है।
वृत्त, जिसकी त्रिज्या के व्युत्क्रम के बराबर वक्रता है, एक वक्र का विहित उदाहरण है। छोटे हलकों में वक्रता अधिक होती है क्योंकि वे अधिक तेजी से झुकते हैं। एक अवकलनीय वक्र के दोलन वृत्त की वक्रता, या वह वृत्त जो इस बिंदु के निकट वक्र का सबसे अच्छा अनुमान लगाता है, वक्र की वक्रता है।
स्पर्शरेखा के विपरीत, जो एक सदिश राशि है, एक बिंदु पर वक्रता आमतौर पर एक अदिश राशि होती है, जिसका अर्थ है कि इसे एक वास्तविक संख्या के रूप में लिखा जा सकता है।
यूक्लिडियन अंतरिक्ष में एम्बेडेड सतहों के लिए वक्रता अधिक जटिल है क्योंकि यह सतह या कई गुना पर चुनी गई दिशा पर निर्भर है।