Table of Contents
Circumference of a Circle
The circumference of a circle is the outer boundary of any shape and the circumference is also known as the perimeter. Every shape has a Circumference of a Circle, the outer periphery that surrounds the circle. We have many geometrical shapes in maths such as triangles, squares, and circles. These shapes are called 2-dimensional shapes. We have 3-dimensional shapes too which are cones, spheres, cylinders, and cubes. These shapes are called 3-dimensional shapes. In this article, we will discuss the circumference of a circle.
Circumference Meaning
The term “circumference” refers to the distance or length around the outer boundary of a closed, curved shape, typically a circle or any other rounded object. It is the measurement of the distance you would travel if you were to walk around the edge of the shape, following its outline.
What is Circumference of a Circle?
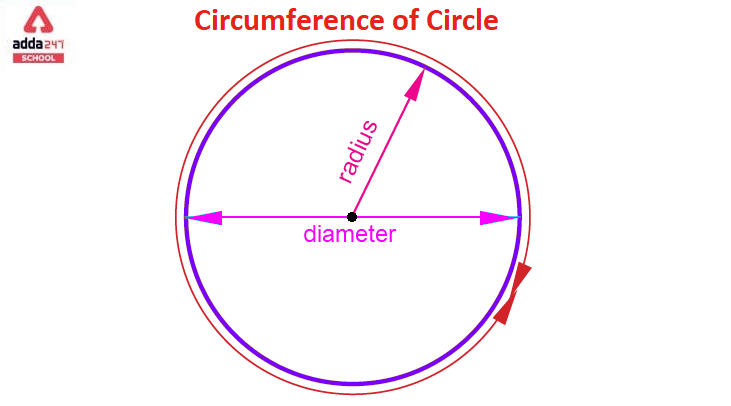
The circumference of a circle is the total length of the boundary or the outer edge of the circle. It can be calculated using the circle’s radius (r) or diameter (d).
The formula for the circumference of a circle is:
Circumference = 2πr
or
Circumference = πd
where:
- C is the circumference of a circle.
- π (pi) is a mathematical constant approximately equal to 3.14159.
- r is the radius of the circle, which is the distance from the center of the circle to any point on the boundary.
- d is the diameter of the circle, which is the distance across the circle passing through the center, and it is equal to 2 times the radius (d = 2r).
So, to find the circumference of a circle, you can use the appropriate formula depending on the information given (either the radius or the diameter).
Circumference of Circle Formula
The circumference of circle is the length of its periphery. Let’s take a look at the components that make up circumference. The three most important elements of a circle are :
Center: The center is located equidistance from every other point on the circle.
Diameter: The diameter of a circle is the distance from the center to the circumference.
Radius: The radius of a circle is the distance between the circle’s center and any point along its perimeter.
| Circumference of a Circle(c) = 2πr |
Where r is the radius of the circle and c is the circumference of the circle. Suppose the radius of the circle is not given the how the circumference of a circle will be calculated?
We know that the radius of the circle is half of the diameter of the circle. If the diameter of a circle is given then also we can find the circumference by putting r = d/2 in the same formula given above.
Circumference of a Circle(c) = 2πr
Substitute radius of circle r = d/2
Circumference Formula of Circle(c) = 2π* (d/2)
| Circumference of a Circle(c) =πd |
Circumference of a Semicircle Formula
A semicircle is the half of the circle i.e. it is formed when we divide the circle into two equal parts. If we are dividing the circle into equal parts then the circumference of the circle will also be divided equally. Let us know the Circumference of the Semicircle.
| Circumference of Semicircle = (πr+2r) |
Here the r is the radius of the circle.
Circumference of a Circle: Solved Examples
Circumference of a circle Example 1: What is the circumference of the circle with a diameter 6 cm?
Solution: In the question, we have given the diameter of the circle, we can find the radius of the circle by putting r = d/2 in the formula of Circumference of Circle.
Circumference Formula of Circle(c) = 2πr
Circumference Formula of Circle(c) = πd
C = (22/7)6
Therefore, Circumference of the Circle(C) = 18.85 cm
Circumference of a circle Example 2: Find the radius of the circle having C = 100 cm.
Solution: In the question, we have given the circumference of the circle and we have to calculate the radius of the circle. We will put this value of circumference in the formula of the circumference of the circle.
Circumference Formula of Circle(c) = 2πr
100 = 2 π r
50 = π r
Therefore, 50 = 22/7* r
The radius of the circle is = 15.90cm
Therefore, the radius of the circle is 15.90cm
Circumference of a circle Example 3: Find the perimeter of a circle whose radius is 9 cm?
Solution: In this question, we have given the radius = 9 cm. And we have to find the circumference of the circle. We have studied the circumference formula above. We will put the value of radius in the circumference formula to calculate the circumference of the circle.
We know that the circumference of a circle = 2πr
Now, substitute the radius value in the circumference formula
C = (2)*(22/7)*(9) cm
C = 56.57cm
Therefore, the circumference of a circle is 56.57 cm.
Circumference of a circle Example 4: Calculate the circumference of the circle in terms of π, whose diameter is 12m.
Solution: In this question, we have given the diameter of the circle which is 12m and we have to calculate the circumference of the circle in terms of π.
We know that, the radius of circle = d/2
Circumference of a circle = 2πr = 2*π*6
C = 2π(6) = 12π m.
Therefore, the perimeter of the circle in terms of π, whose diameter is 12 cm is 12π m.
Circumference of a circle Example 5: Find the perimeter of a circle whose radius is 13 cm?
Solution: In this question, we have given the radius = 13 cm. And we have to find the circumference of the circle. We have studied the circumference formula above. We will put the value of radius in the circumference formula to calculate the circumference of the circle.
We know that the circumference of a circle = 2πr
Now, substitute the radius value in the circumference formula
C = (2)*(22/7)*(13) cm
C = 81.71 cm
Therefore, the circumference of the circle is 81.71 cm.
Circumference of a circle Example 6: Calculate the circumference of the circle in terms of π, whose diameter is 20m.
Solution: In this question, we have given the diameter of the circle which is 20m and we have to calculate the circumference of the circle in terms of π.
We know that, the radius of circle = d/2 = 20/2 =10
Circumference of circle = 2πr = 2*π*10
C = 2π(10) = 20π m.
Therefore, the perimeter of the circle in terms of π, whose diameter is 20 cm is 20π m.
Radius of a Circle Definition for Class 9
The radius of a circle is a fundamental geometric concept that refers to the distance from the center of the circle to any point on its circumference (the outer boundary or edge). It is denoted by the letter “r” and is usually measured in units of length, such as centimeters (cm), meters (m), or inches (in).
In mathematical terms, if you have a circle with a center point (O) and a point on its circumference (A), the radius (r) is the line segment that connects the center (O) to the point on the edge (A). The length of this line segment represents the radius of the circle.
The radius plays a crucial role in various geometric calculations, including finding the circumference, area, and diameter of a circle. It is half the length of the diameter, and the formula for calculating the circumference of a circle is:
Circumference (C) = 2 * π * radius (r)
Related Posts:

 MBOSE Routine 2025 Out, Check Meghalaya ...
MBOSE Routine 2025 Out, Check Meghalaya ...
 Best NEET Offline Test, Check NEET ANKLA...
Best NEET Offline Test, Check NEET ANKLA...
 JEE Advanced 2025 Exam Date Out, Online ...
JEE Advanced 2025 Exam Date Out, Online ...






























