Table of Contents
The CBSE will conduct the class 12th board examination from February 15 to April 4, 2025. During this period, the Mathematics exam will be held on March 8, 2025. With less tie remaining for the exam, students should now focus on solving important previous year questions. To help board students, we have provided Class 12 Mathematics Linear Programming Most Important Previous Year Questions with Solutions PDF on this page.
Class 12 Mathematics Linear Programming Most Important Previous Year Questions with Solutions
The Class 12 Maths Linear programming PYQs provided here has been asked frequently in the exam. Solving these important questions of the Class 12 Mathematics Linear Programing will help students to score full marks in this chapter. The Mathematics board exam paper will definitely have questions from the Linear Programming concept. Go through the questions and answers of LPP to ensure you successfully solve board exam questions from this chapter.
Class 12 Maths Linear Programming Important Previous Year Questions with Solutions
The important short answer type questions and long answer type important questions from Class 12 Maths Linear Programming chapter has been given below with solutions. Students should remember that questions in the board exam paper will be based on the concepts present in the following questions.
Q1. The point which lines in the half-plane 2x+y-4≤0 is
(a) (0, 8)
(b) (1, 1)
(c) (5, 5)
(d) (2, 2)
Q2. The common region determined by all the constraints of a linear programming problem is called:
(a) An unbounded region
(b) An optimal region
(c) A bounded region
(d) A feasible region
Q3. The number of corner points of the feasible region determined by constraints x-y≥0, 2y≤x+2, x≥0, y≥0 is:
(a) 2
(b) 3
(c) 4
(d) 5
Q4. If the minimum value of an objective function z=ax+by occurs at two points (3,4) and (4,3) then
(a) a+b=0
(b) a=b
(c) 3a=b
(d) a=3b
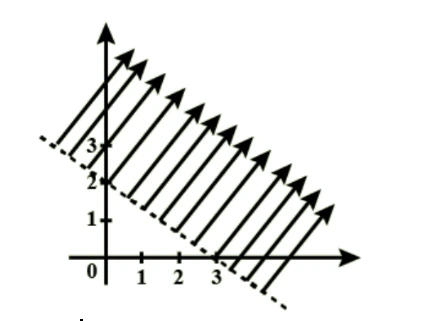
Q5. The graph of the inequality 2x+3y>6 is
(a) Half plane that contains the origin
(b) Half plane that neither contains the origin nor the points of the line 2x+3y=6.
(c) Whole XOY-plane excluding the points on the line 2x+3y=6.
(d) Entire XOY-plne.
Q6. Find the maximum value of z=3x+4y subject to the constraints x≥0, y≥0 and x+y≤1.
Q7. If the corner points of the feasible region of an LPP are (0,3), (3,2) and (0,5), then find the minimum value of z=11x+7y.
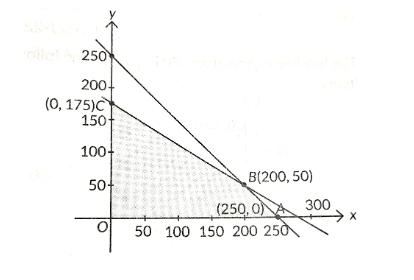
Q8. The corner points of the bounded feasible region of an LPP are O(0,0), A(250,0), B(200,50) and C(0,175). If the maximum value of the objective function Z=2ax+ by occurs at the points A(250,0) and B(200,50), then find the relation between a and b.
Q9. Solve the following linear programming problem graphically:
Maximise z=2x+3y
Subject to the constraints
x+y≤6
x≥2
y≤3
x≥0,y≥0
Q10. Solve graphically the following linear programming problem:
Maximise z=6x+3y,
Subject to the constraints
4x+y≥80,
3x+2y≤150,
x+5y≥115,
x≥0, y≥0.
Q11. Solve the following linear programming problem graphically.
Minimize: Z=60x+80y
Subject to constraints:
3x+4y≥8
5x+2y≥11
x, y≥0
Q12. Solve the following LPP graphically:
Minimize z=5x+7y
Subject to the constraints
2x+y≥8, x+2y≥10, x,y≥0
Q13. Solve the following L.P.P. graphically: Minimise: Z=6x+3y
Subject to constraints:
4x+y≥80;x+5y≥115;
3x+2y≤150; x,y≥0.
Q14. Solve the following linear programming problem graphically.
Maximize: P=70x+40y
Subject: 3x+2y≤9, 3x+y≤9, x≥0, y≥0.
Q15. Solve the following linear programming problem graphically:
Maximize z=3x+9y
Subject to constraints
x+3y≤60
x+y≥10
x≤y
x,y≥0
Solutions
The solutions to the above-mentioned questions have been provided by experts with step-by-step explanation that will help students get conceptual clarity to score full marks.
S1. Ans.(b)
Sol. Substitute x=1 and y=1 in 2x+y≤4
⇒21+1≤4⇒3≤4 which is true.
So, (1,1) lies in the half plane 2x+y-4≤0
S2. Ans.(d)
Sol. The common region determined by all the constraints of a linear programming problem is called feasible region.
S3. Ans.(a)
Sol. We have, x-y≥0, 2y≤x+2, x≥0 and y>0.
Let us draw the graph of given constraints we get
x-y=0
| x | 0 | 1 |
| y | 0 | 1 |
And 2y=x+2
| X | 0 | -2 |
| y | 1 | 0 |
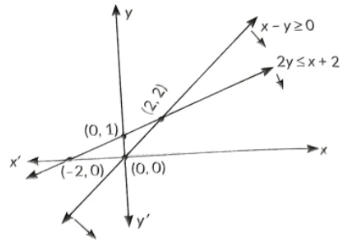
The feasible region is unbounded.
∴ There are two corner points as (0,0) and (2,2).
S4. Ans.(b)
Sol. Since, minimum value of Z=ax+by occurs at two points (3,4) and (4,3).
∴ 3a+4b=4a+3b⇒a=b
S5. Ans.(b)
Sol. From the graph of inequality 2x+3y>6. It is clear that it does not contain the origin nor the points of the line 2x+3y=6
S6.
Sol. We have to maximise Z=3x+4y
Subject to constraints, x≥0, y≥0 and x+y≤1
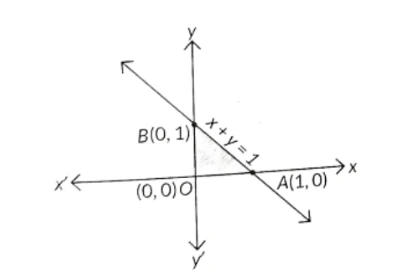
The shaded portion OAB is the feasible region, where 00,0, A(1,0) and B(0,1) are the corner points.
At O 0,0, Z=3×0+4×0=0
At A 1,0, Z=3×1+4×0=3
At B 0,1, Z=3×0+4×1=4
∴ Maximum value of Z is 4, which occurs at B0,1.
S7.
Sol. Given, Z=11x+7y
At 0, 3 Z=11×0+7×3=21
At 3, 2, Z=11×3+7×2=47
At 0, 5, Z=11×0+7×5=35
Thus, Z is minimum at (0, 3) and minimum value of Z is 21.
S8.
Sol. Given Z=2ax+by …(i)
Putting x=250 and y=0 in (i) we get
Zmax 2a 250+b0=500a …(ii)
Putting x=200 and y=50 in (i) we get
Zmax=2a200+b50=400a+50b
From (ii) and (iii), we get 500a=400a+50b
⇒100a=50b⇒2a=b
S9.
Sol. Consider the graph given below:
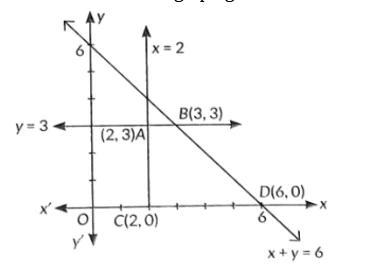
Corner points are A(2,3), B(3,3), C(2,0) and D(6,0)
ZA=4+9=13
ZB=6+9=15
Zc=4
ZD=12
Maximum value of z is 15 at (3,3).
S10.
Sol. We have, z=6x+3y
Subject to constraints
4x+y≥80
3x+2y≤150
x+5y≥115
x≥0, y≥0
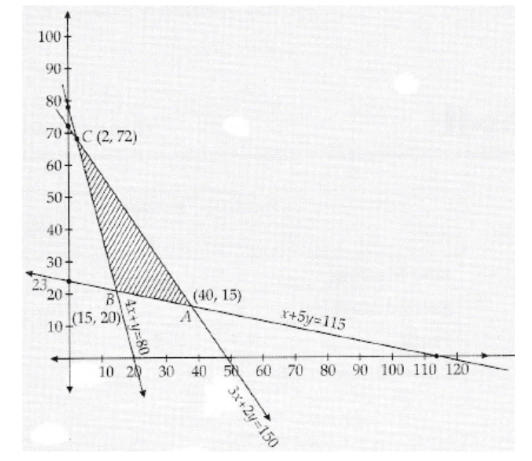
∴ The corner points are (2, 72), (15, 20) and (40,15)
| Corner points | z=6x+3y |
| (2, 72) | z=6×2+3×72=228 |
| (15,20) | z=6×15+3×20=150 |
| (40,15) | z=6×40+3×15=228 |
∴ The maximum value of z=6x+3y is 285 at the corner point (40,15).
S11.
Sol. We have, min z=60x+80y:
Subject to constraints:
3x+4y≥8, 5x+2y≥11;x,y≥0
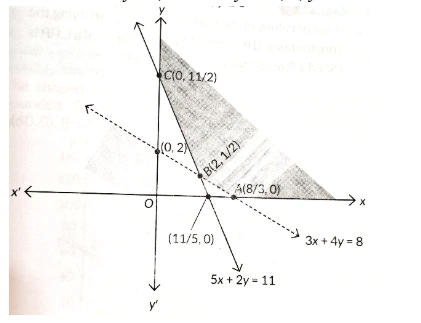
From graph, it is clear that feasible region is unbounded.
The corner point of the feasible region are A(8/3, 0),
B(2, 1/2) and C(0, 11/2).
The value of Z at these corner points are as follows:
| Corner Points | Z=60x+80y |
| A(8/3,0) | 160 |
| B(2,1/2) | 160 |
| C(0,11/2) | 440 |
As the feasible region is unbounded,
∴ 60 may or may not be the minimum value of Z. So, we graph the inequality 60x + 80y < 160 i.e., 3x + 4y < 8 and check whether the resulting half plane has points in common with the feasible region or not. From graph, it can be seen that feasible region has no common point with 3x + 4y < 8
∴ Minimum value of Z is 160 at the line joining the points (8/3,0) and (2, 1/2).
S12.
Sol. We have minimize z=5x+7y,
Subject to constraints, 2x+y≥8, x+2y≥10, x,y≥0
To solve LPP graphically we convert inequations into equation.
Now, l1:2x+y=8, l2:x+2y=10 and x=0y=0
l1 and l2 intersect at E(2,4).
Let us draw the graph of these equation as shown below
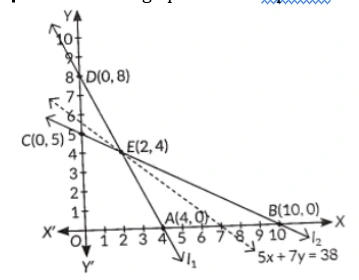
The corner points of the feasible region are D(0, 8), B(10,0) and E(2,4).
| Corner points | Value of z=5x+7y |
| D(0,8) | 56 |
| B(10,0) | 50 |
| E(2,4) | 38 (Minimum) |
From the table, we find that 38 is the minimum value of z at E(2,4). Since the region is unbounded, so we draw the graph of inequality 5x + 7y < 38 to check whether the resulting open half plane has any point common with the feasible region. Since it has no point in common. So, the minimum value of z is obtained at E(2,4) and the minimum value of z = 38.
S13.
Sol. Given, L.P.P.
Minimise, Z=6x+3y
Subject constraints:
4x+y≥80;x+5t≥115;3x+2y≤150, x,y≥0
Graph of the lines 4x+y=80, x+5y=115 and 3x+2y=150 is given below.
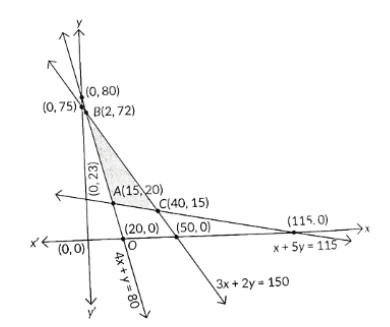
Intersecting point of lines x+5y=115 and 4x+y=80 is A(15,20).
Intersecting point of lines 3x+2y=150 and 4x+y=80 is B(2,72).
Intersecting point of lines 3x+2y=150 and x+5y=115 is C(40,15).
∴ The corner points of the feasible region ABC are A(15,20), B(2,72) and C(40,15)
The value of Z is these points are as follows:
| Corner point | Z=6x+3y |
| A(15,20) | 6×15+3×20=150← Minimum |
| B(2,72) | 6×2+3×72=228 |
| C(40,15) | 6×40+3×15=285 |
S14.
Sol. Given
Maximize: P=70x+40y
Subject to
3x+2y≤9, 3x+y≤9, x≥0, y≥0
3x+2y=9……..(i)
3x+y=9 ……….(ii)
From equation (i), we get (3, 0) and (0, 9/2)
From equation (ii), we get (3, 0) and (0, 9)
Corner points of the feasible region are O(0, 0), A(3, 0) and B(0, 9/2)
| Corner points | Value of Z |
| O(0, 0) | Z = 0 |
| A(3, 0) | Z = 210 (maximum) |
| B(0, 9/2) | Z = 180 |
S15.
Sol. We have maximize z=3x+9y
Subject to constraints x+3y≤60, x+y≥10, x≤y,x,y≥0
To solve L.P.P. graphically we convert inequations into equations.
l1:x+3y=60, l2:x+y=10, l3:x=y, x=0 and y=0
l2 and l3 intersect at (5, 5). l1 and l3 intersect at (15, 15). The shaded region ABCD is the feasible region and is bounded. The corner points of the feasible region are A(0, 10), B(5, 5), C(15, 15) and D(0, 20)
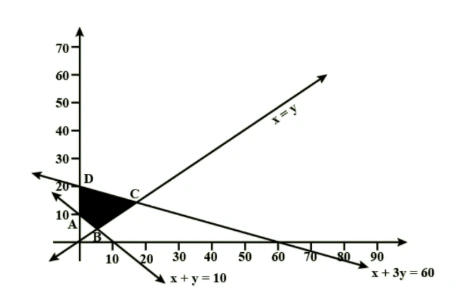
| Corner points | Value of z=3x+9y | |
| A(0,10) | 90 | |
| B(5,5) | 60 | |
| C(15,15) | 150 | Maximum (Multiple optimal solutions) |
| D(0,20) | 150 | |
The maximum value of Z on the feasible region occurs at the two corner points C(15,15) and D(0,20) and it is 180 in each case.


 Greater Than and Less Than, Equal to Sig...
Greater Than and Less Than, Equal to Sig...
 CBSE Date Sheet 2025 Out, Download Class...
CBSE Date Sheet 2025 Out, Download Class...
 CBSE Accountancy Exam 2025 Update - Are ...
CBSE Accountancy Exam 2025 Update - Are ...




