Critical Angle: Definition, Formula, Derivation, Examples for Class 10, 12

Critical angle is one of the most important topics in physics which is related to the world of optics. This angle’s notion has a prominent position in the field of optics, where light rays move and interact with various materials. This phenomenon occurs when light changes from one medium to another, offering information on how light behaves under particular circumstances. This phenomenon is related to the refraction of light, one of the two most important processes associated with the property of light, the other being reflection.

What is Critical Angle?

Critical Angle is the critical value of the angle of incidence beyond which the phenomenon of Total Internal Reflection (TIR) takes place. It can be observed during the light’s refraction process. It is also known as the critical value of the incident angle, above which the total internal reflection takes place.

Refraction is the phenomenon that occurs when the medium through which light is transmitted changes, changing the direction in which the light will propagate. Light changes direction and bends towards the normal if it enters a denser medium from one that is relatively rarer. This normal line is a fictitious perpendicular line constructed at the point where light meets the boundary of two media.

Critical Angle Definition

Formally, the it is the angle of incidence at which the angle of refraction becomes perpendicular, i.e., 90°. In other words, critical angle is the angle of incidence that produces 90° angle of refraction. This special angle is defined for a pair of medium and it changes when one of the medium changes. At this angle, the light rays travel along the boundary of the two media, perpendicular to the normal line. It is generally denoted by θ_c or i_c. Let us understand this concept through a diagram.

Critical Angle Diagram

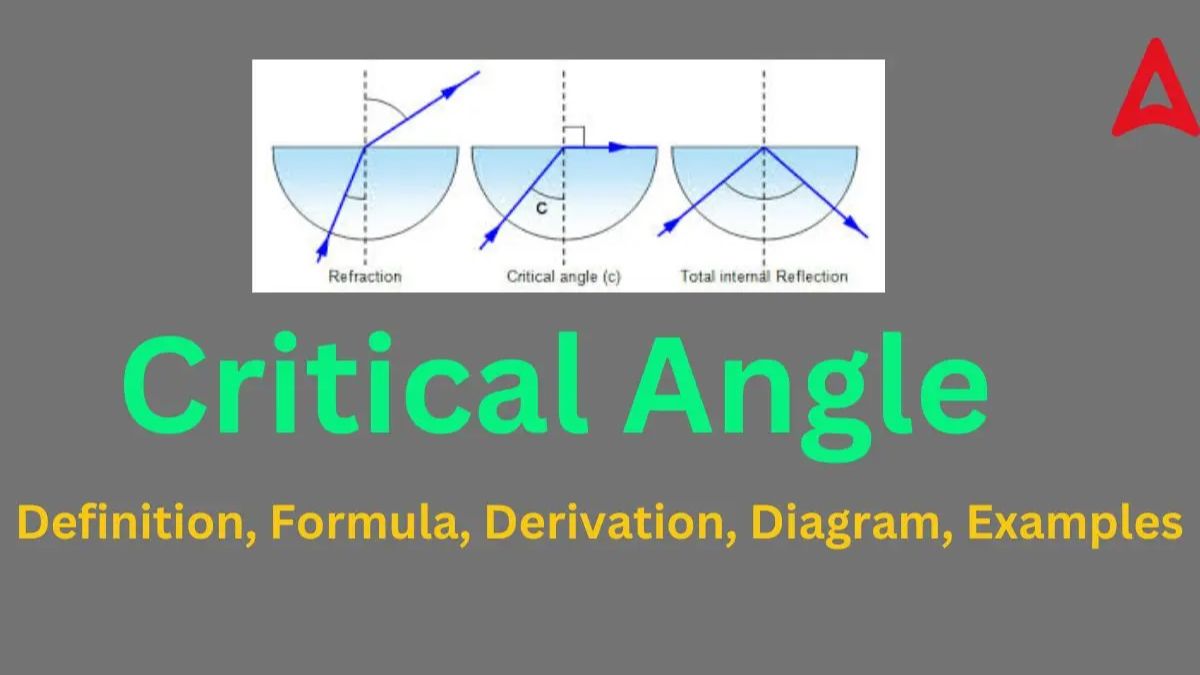
The concept of this angle can be best understood with the help of a diagram. The diagram given below will give you a clear understanding of the concept related to this angle.

From the above figure, we can clearly visualize that in the first condition at certain incident angle θ₁, the refracted ray makes an angle theta 2 with the normal which is less than 90°.

But as we keep on increasing the incident angle, there comes a point when the refracted ray becomes 90° to the normal, as in the 2nd condition. This incident angle is known as the critical angle denoted by θc.

Beyond the critical value, the light rays are deviated back into the same medium from which it travelled, as shown in the third case.

Critical Angle of Refraction

This angle is precisely known as the critical angle of refraction. It is due to the fact that it is associated with the refraction of light. It must be noted that this special angle of refraction is the incident angle, i.e., the angle subtended by the light ray in the 1st medium. This angle’s concept is valid if and only if the light rays are travelling from a dense medium to a rarer medium. It is because, only in this case the light rays are bent away from the normal.

Critical Angle Formula

The formula to derive the critical value of the incident angle is based on the Snell’s law of refraction. This formula takes into account the refractive index of both the medium. By knowing these basic concepts, students can understand the terms given in the this formula quite easily.

The formula for this angle is given by

θ_c = Sin^-1(n₂/n₁)

where, θ_c is the critical value of the incident angle

n₁ is the refractive index of the incident medium or denser medium

n₂ is the refractive index of the refracted medium or rarer medium

Critical Angle Equation

The formula mentioned for this special angle above is also commonly known as the critical incidence angle equation. This equation is used to derive the critical value for a given pair of media at a particular light frequency after which the phenomenon of total internal reflection takes place. It must be noted that the value of this angle changes when we change either the frequency of the light or the pair of media. So we can say that this equation is given by:

θ_c = Sin^-1(n₂/n₁)

or,

i_c = Sin^-1(n₂/n₁)

where θ_c or i_c is the critical value of the incident angle

Derivation of Critical Angle

The formula to derive the critical value of the incident angle can be found using the Snell’s law. Before deriving the formula, let us first understand the definition of Snell’s law. Snell’s law states that for a pair of media, the ratio of the sine of incidence angle to the sine of the refraction angle for a particular light color.

It tells about the relationship between incidence and refraction angle and introduces the concept of refractive index, denoted by n. It is the property of a medium which shows its light bending ability.  Knowing these terms, let us derive the formula to derive this special angle with the help of the diagram given below.

As given in the above figure,

n₁ is the refractive index of the incident or denser medium

n₂ is the refractive index of the of the refracted medium or rarer medium

Let us suppose at angle the incidence angle θ₁, the refracted ray makes angle θ₂ with the normal.

So using the Snell’s law we can write

n₁Sinθ₁ = n₂Sinθ₂ ——————- (1)

When the angle of incidence becomes critical angle, i.e. i_c, the angle of refraction becomes 90°

i.e., when θ₁ = i_c, then θ₂ becomes 90°

Putting these values in equation 1, we get

n₁Sini_c = n₂Sin90°

as sin90° = 1

So, n₁Sini_c = n₂ x 1

n₁Sini_c = n₂

or, Sini_c = n₂/n₁

Hence, i_c = Sin^-1(n₂/n₁)

Critical Angle and Total Internal Refraction

The critical incidence angle concept explains the special phenomenon of the total internal reflection. Total internal reflection is the reflection of the light rays back to the same medium from which it was traveling. It v occurs at the boundary of the two media. As stated in the case of this special angle, it occurs only when the light rays travel from a denser medium to the rarer medium.

If the angle of incidence exceeds the the critical value for a pair of media, the phenomenon of total internal reflection takes place. In other words, the total internal reflection takes place when the incidence angle of the light rays are above the the critical value for a pair of media.

Mathematically, for total internal reflection to take place, the incidence angle must satisfy the following condition:

θ > θc

Where, θ  is the angle of incidence

θc is the critical value

Critical Angle of Diamond

We can calculate the critical value of the angle of diamond by knowing its refractive index. As the refractive index of the diamond is 2.42, we can calculate its critical value after which the total internal reflection takes place.

We generally calculate the absolute value of this angle of an object with respect to vacuum or air. The refractive index for both vacuum or air is taken as 1

So, n1 = refractive index of diamond (denser medium) = 2.42

n2 = refractive index of air/vacuum (rarer medium) = 1

As by using the formula for critical incidence angle, we get

θc = Sin^-1(n2/n1)

θc = Sin^-1(1/2.42)

On solving we get,

θc = 24°

Critical Angle of Water

As we know, the refractive index of water is 1.33

So using this knowledge, we can derive its critical value with respect to air

n1 = refractive index of water (denser medium) = 1.33

n2 = refractive index of air (rarer medium) = 1

As by using the formula for critical value, we get

θc = Sin^-1(n2/n1)

θc = Sin^-1(1/1.33)

On solving we get,

θc ≈ 49°

Critical Angle of Glass

The refractive index of glass is known to be 1.52

So using this knowledge, we can derive its critical incidence angle with respect to air/vacuum

n1 = refractive index of water (denser medium) = 1.52

n2 = refractive index of air/vacuum (rarer medium) = 1

As by using the formula for this special angle, we get

θc = Sin^-1(n2/n1)

θc = Sin^-1(1/1.52)

On solving we get,

θc ≈ 41.1°

Critical Angle Properties

It is utmost important to learn the properties of this special angle. These properties are very important from examination point of view, especially for class 10 and class 12 students. This topic is very much important for class 10 and 12 students. These properties will help them understand different aspects of this special angle. Some of tis properties are:

• Lower value of this angle corresponds to high light bending ability of the pair of media
• the value of this angle remains constant for a pair of media for a particular light frequency
• This concept is valid only if the light travels from a denser medium to rarer medium
• Total internal reflection takes place only if the incidence angle is more than the critical incidence angle

Critical Angle Examples

Some of the solved questions on this topic is given below. These solved examples will give a clear idea to the students about how to use the knowledge of these concepts in solving various problems in the optical refraction domain.

Example 1: Given an optical fiber with a refractive index of 1.5. The light is passed into the optical fiber from the surrounding air with a refractive index of 1. At what condition, will the total internal reflection takes place in this case?

Solution: As we know that for the total internal reflection to occur:

incidence angle > critical incidence angle

Let it be θc

Using the formula,

θc = Sin^-1(n2/n1)

Here, n1 = refractive index of the denser medium, i.e., fiber = 1.5

n2 = refractive index of the rarer medium , i.e., air = 1

So, θc = Sin^-1(1/1.5)

θc = Sin^-1(0.667)

Hence, θc ≈ 41.8°

So, the incidence angle must be greater than 41.8° for the total internal reflection to take place.

Example 2: The refractive of the denser medium is 2 while the refractive index of the rarer medium is 1. What will be the critical incidence angle for this pair of media?

Solution: As we have been given

n1 = 2

n2 = 1

By using the equation θc = Sin^-1(n2/n1), we get

θc = Sin^-1(n2/n1)

or, θc = Sin^-1(1/2)

Hence θc = 30°

Sharing is caring!