Differentiation of Tan Inverse x – Explanation, Formula, Examples

The concept of differentiation touches almost all branches of Physics and Mathematics. The differentiation of Tan inverse x is one such concept that is related to inverse trigonometry. Tan inverse x (Tan^-1x) is one of the six trigonometry ratios besides Sin^-1, Cos^-1, Cosec^-1, Sec^-1, and Cot^-1. The differentiation of Tan^-1x is also called the Derivative of Tan inverse x. Tan inverse is basically an inverse of the trigonometry ratio Tan. In this article, we will explore different aspects of the derivative of Tan inverse x including its proof.

Differentiation of Tan Inverse x

Tan^-1x or arctan(x) stands for the inverse tangent function, also referred to as the arctangent function. It is the inverse of the tangent function, which means that like all other inverse trigonometry functions, it outputs the angle rather than the tangent of an angle. All real numbers x are defined by the inverse tangent function. The differentiation of Tan inverse x implies how fast the function Tan inverse changes with respect to another parameter x. It is denoted by d(Tan^-1x)/dx. Its differentiation formula can be found using different methods. Let us understand its formula and derivation in depth.

Differentiation of Tan Inverse x Formula

The differentiation of Tan^-1x gives the value of angle at which the Tan will show that value. As stated earlier, the derivative of Tan^-1x will be denoted by d(Tan^-1x)/dx, where dx means we are differentiation with respect to x. The formula for the same is given below.

The differentiation of Tan inverse x is given by:

d(Tan^-1x)/dx = 1/(1 + x²)

where, x is the angle value

Double Differentiation of Tan Inverse x

Double differentiation means when we differentiate the result of first derivation again. It is also known as double order derivative of Tan inverse x. It is denoted by d²(Tan^-1x)/dx. If a function f(x) is given then the double differentiation may be denoted as f”(x) or d²(f(x))/dx. So, the double differentiation of second order derivative of Tan Inverse x will be given by:

d²(Tan^-1x)/dx = -2x/(1+x²)²

Differentiation of Tan Inverse x Proof

We can find the above mentioned formula for the derivation of Tan Inverse x by suing concepts of mathematics. The derivation for the same is explained below.

We have been given f(x) = tan^-1x

Let y = tan^-1x

Multiplying by tan on both sides, we get

tan(y) = tan (tan^-1x)

so, tan y = x ——— (i)

On differentiating equation (i) with respect to x

(dx/dx) =d(tan y)/dx

=> 1 = [d(tan y)/dx]

Multiplying and dividing by ‘dy’ in RHS

=> 1 = [d(tan y)/dx] × [dy/dy]

=> 1 = [d(tan y)/dy] × [dy/dx]

as, d(tanx)/dx = sec²x

so, 1 = [sec²y] dy/dx

using formula sec²x = 1 + tan²x, we get

=> 1 = [1 + tan²y] dy/dx

or, dy/dx = [1] / [1 + tan²y] ————-(ii)

Substituting tan y = x (from equation (i)) into equation (ii), we get

dy/dx = 1 / (1 + x²)

Hence,  d(tan^-1x)/dx = 1 / (1 + x²)

Derivative of Tan Inverse x Graph

We can represent the behavior of the differentiation of tan inverse x graphically. The graph for the same is illustrated below.

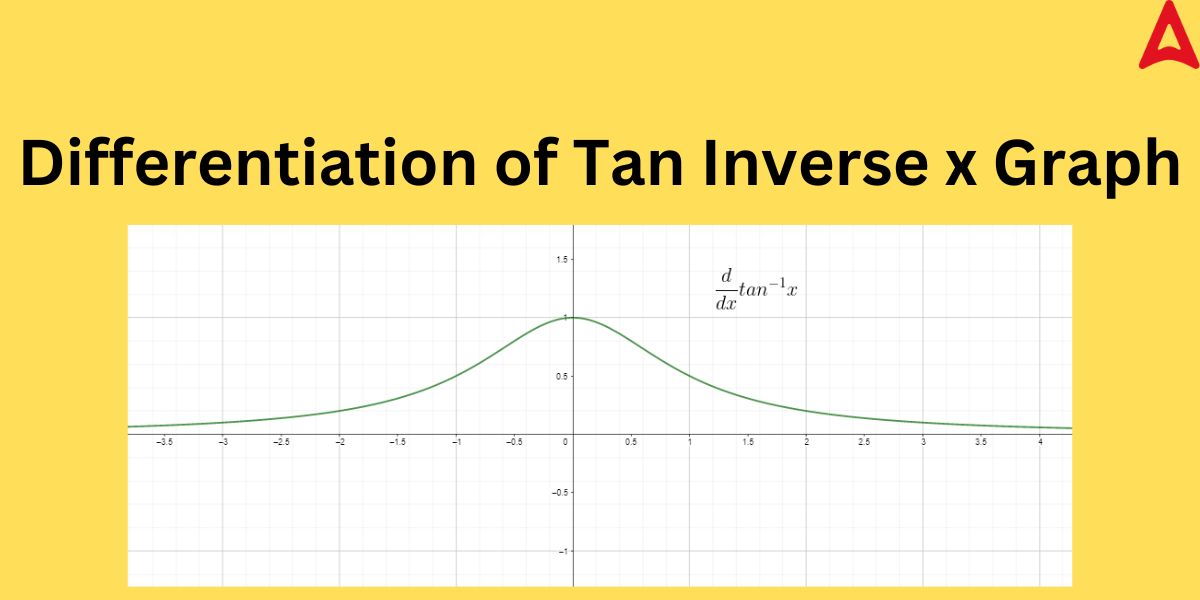
As we can observe from the above example that the differentiation graph of tan inverse that the graph is bell-shaped. It means the value of its differentiation increases at the center and decreases gradually on both sides of the x-axis.

Differentiation of Tan Inverse x Using First Principle

We can find out the derivative of tan inverse using the first principle. The first principle rule is one of the most important concepts in the derivative proof. The proof of this formula using this rule is given below.

Given f(x) = tan^-1x

f(x+h) = tan^-1(x+h)

According to the first order principle, the derivative of f(x) is given by:

f'(x) = lim_h—>0 [f(x+h)-f(x)]/h

substituting the relevant values, we get

f'(x) = lim_h—>0 [tan^-1(x+h)-tan^-1x]/h

as we know, tan^-1x – tan^-1y = tan^-1[(x – y)/(1 + xy)]

so, f'(x) = lim_h—>0 [tan^-1[(x+h-x)/(1 + (x+h)x)]/h

Multiplying the denominator of the above equation by (1 + (x+h)x), we get

f'(x) = lim_h—>0 [tan^-1[(x+h-x)/(1 + (x+h)x)]/h x [(1 + (x+h)x)/(1 + (x+h)x)]

or, f'(x) = lim_h—>0 [tan^-1[(h)/(1 + (x+h)x)]/[(1 + (x+h)x)x h/(1 + (x+h)x)]

or, f'(x) = lim_h—>0 1/(1 + (x+h)x) . lim_h—>0 [tan^-1[(h)/(1 + (x+h)x)]/ h/(1 + (x+h)x)

as, lim_h—>0 tan^-1x/x = 1

so, lim_h—>0 1/(1 + (x+h)x) . 1

putting the value of limit, we obtain

1/(1 + (x+0)x)

Hence, f'(x) = 1/1 + x²

Differentiation of Tan Inverse x Class 12

The derivative of tan inverse function is one of the most important concepts in class 12 mathematics. Students are asked about its formula, proof and examples based on this concept. Some important concepts on this topic for class 12 students is given below.

• The differentiation of tan^-1x is given as 1/1 + x²
• The value of the derivative of tan inverse x is always negative that of the cot inverse x
• The anti derivative value of tan inverse x will be equal to its integration value

Differentiation of Tan Inverse x Examples

Some of the solved examples on the concept of tan inverse x differentiation topic is given below. These solved questions will help students understand this concept in a better way.

Example 1: Find the derivative of tan^-1x².

Solution: Given f(x) = tan^-1x²

Let y = tan^-1x²

or, tan(y) = x²

Differentiating with respect to x, we get

d(tan(y))/dx = d(x²)/dx

sec²y . dy/dx = 2x

or, dy/dx = 2x/sec²y

as 1 + tan²x = sec²x

so, 2x/(1 + tan²y)

as x² = tany

so, 2x/(1 + (x²)²)

Hence, 2x/1 + x⁴

Example 2: Find the derivation of tan^-12x

Solution: given f(x) = tan^-12x

let, y = tan^-12x

tany = 2x

on differentiating both sides with respect to x

d(tany)/dx = d(2x)/dx

as d(tanx)/dx = sec²x

sec²y . dy/dx = 2

dy/dx = 2/sec²y

as sec²x = 1 + tan²x

so, dy/dx = 2/1 +tan²y

as tany = 2x

so, dy/dx = 2/1 + (2x)²

or, dy/dx = 2/1 + 4x²

Example 3: What will be the value of the differentiation of tan^-13x

Solution: Given, tan^-13x

as d(tan^-1x)/dx = 1/1 + x²

Here, x = 3x

putting x = 3x in the derivative formula, we get

1/1 + (3x)²

= 1/1 + 9x²

so, the differentiation of tan^-13x will be equal to 1/1 + 9x²

Sharing is caring!