Kirchhoff’s laws Formula, Equation, Examples

Kirchhoff’s law: Kirchhoff’s circuit laws are at the foundation of circuit analysis. With these rules plus the equations for individual components (resistor, capacitor, and inductor), we have the primary instrument to begin analysing circuits. In this post, we will look at Kirchhoff’s current and voltage laws and how to apply them to circuit analysis.

Kirchhoff’s laws

Kirchhoff’s laws are two circuit analysis laws named after Gustav Kirchhoff. They are used to analyse electrical circuits and solve for unknown currents and voltages. Kirchhoff’s current law (KCL) stipulates that all currents entering a node must equal the sum of all currents exiting the node. This law is a result of charge conservation.
Kirchhoff’s voltage law (KVL) asserts that the sum of the voltage drops around each closed loop in a circuit must equal zero. This law is a result of energy conservation. Kirchhoff’s rules can be used to solve for any unknown current or voltage in a circuit. They are a potent tool for circuit analysis and are utilised by engineers and scientists in various domains.
Here is a formula for Kirchhoff’s current law:

∑In = ∑Iout

Kirchhoff’s Laws History

Gustav Robert Kirchhoff was a German physicist who made substantial contributions to the disciplines of electrical circuits, spectroscopy, and thermal radiation. He is well known for his two circuit analysis principles, which are used to solve unknown currents and voltages in electrical circuits.Kirchhoff was born on March 12, 1824, in Königsberg, Prussia (now Kaliningrad, Russia). He studied mathematics and physics at the University of Königsberg, where he was a pupil of Franz Neumann. Kirchhoff became a Privatdozent (unpaid lecturer) at the university after graduating in 1847. Kirchhoff’s two laws of circuit analysis were published in 1848. These rules are now known as Kirchhoff’s current law (KCL) and Kirchhoff’s voltage law (KVL). According to KCL, the sum of the currents entering a node must match the sum of the currents exiting the node. According to KVL, the sum of the voltage drops around any closed loop in a circuit must equal zero. Kirchhoff was named professor of physics at the University of Heidelberg in 1854. He worked on the spectroscope with Robert Bunsen in Heidelberg. A spectroscope is a device that can be used to analyse the light emitted by a substance. Kirchhoff and Bunsen utilised the spectroscope to detect elements in the Sun and other stars. They also discovered the elements caesium and rubidium. Kirchhoff made contributions to the field of thermal radiation in addition to his work on electrical circuits and spectroscopy. In 1859, he published a thermal radiation law that states that the intensity of thermal radiation radiated by a blackbody is proportional to the fourth power of its absolute temperature. This is now known as Kirchhoff’s law of thermal radiation. Kirchhoff died on October 17, 1887, in Berlin, Germany. He was a well-regarded physicist who made substantial contributions to a variety of subjects. His work on electrical circuits, spectroscopy, and thermal radiation is still used by scientists and engineers all around the world.

Kirchhoff’s First law/ Kirchhoff’s current law (KCL) for Class 12

Kirchhoff’s first law, commonly known as Kirchhoff’s current law (KCL), is a fundamental statement of circuit analysis that asserts that the algebraic total of all currents entering and leaving a node must equal zero. This law is a result of charge conservation.

In other words, KCL specifies that the entire amount of charge flowing into a node must match the total amount of charge flowing out of that node. This is because charge cannot be created or destroyed; it can only be transferred.

KCL can be used to solve for unknown currents in a circuit. To do so, you must first identify all of the nodes in the circuit. After you’ve identified the nodes, you can apply KCL to each one.

Consider the circuit depicted below,circuit with three nodes

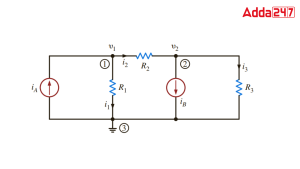
The goal is to find the current I1.

At node A, we can utilise KCL to solve for I1. Kirchhoff’s current law states that the sum of all currents entering a node must equal the sum of all currents exiting the node. Three currents enter node A: I1, I2, and I3. We also have no currents leaving the node.

I1 + I2 + I3 = 0
We can also utilise KCL at node B. Kirchhoff’s current law states that the sum of all currents entering a node must equal the sum of all currents exiting the node. We have one current entering node B: I3. We also have two currents leaving the node: I4 and I5.

I3 = I4 + I5
We can now solve for I1. Substituting I3 into the equation at node A yields:

I1 + I2 + (I4 + I5) = 0
This equation can be solved for I1:

I1 = -(I2 + I4 + I5)
To summarise, Kirchhoff’s first law is a strong technique that may be used to solve unknown currents in electrical circuits. It is a result of charge conservation, and it may be applied to any circuit, regardless of its complexity.

Kirchhoff’s Current law formula

The algebraic sum of all currents entering and leaving a node must equal zero, according to Kirchhoff’s current law (KCL). This law is the result of charge conservation.

The formula for Kirchhoff’s current law is:

∑Iin = ∑Iout

Where:

• ∑Iin is the sum of all currents entering the node
• ∑Iout is the sum of all currents leaving the node

Kirchhoff’s second law/ Kirchhoff’s voltage law (KVL) for Class 12

Kirchhoff’s second law, often known as Kirchhoff’s voltage law (KVL), is a fundamental statement of circuit analysis that asserts that the algebraic sum of the voltage drops around each closed loop in a circuit must equal zero. This law is a result of energy conservation.

In other words, KVL specifies that the entire amount of energy lost in a circuit must equal the total amount of energy received in that circuit. This is because energy cannot be generated or destroyed; it can only be transferred from one form to another.

KVL can be used to solve for unknown voltages in a circuit. To begin, identify all of the loops in the circuit. Once you’ve discovered the loops, you may apply KVL to each one.

Consider the circuit depicted below.

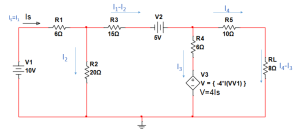
The goal is to determine V1.

KVL around loop 1 can be used to solve for V1. Kirchhoff’s voltage law asserts that the algebraic total of voltage drops around every closed loop in a circuit must equal zero. There are two voltage decreases around loop 1: V1 and V2.

V1 – V2 = 0
We can also utilise KVL around loop 2. Kirchhoff’s voltage law asserts that the algebraic total of voltage drops around every closed loop in a circuit must equal zero. There is one voltage drop around loop 2: V3.

V3 = 0
We can now solve for V1. When we substitute V3 into the equation at loop 1, we get:

V1 – V2 = 0
This equation can be solved for V1:

V1 = V2
To summarise, Kirchhoff’s second law is a strong technique that may be utilised to solve for unknown voltages in electrical circuits. It is a result of energy conservation, and it may be applied to any circuit, regardless of its complexity.

Limitations of Kirchhoff’s laws

Here are some of Kirchhoff’s laws’ limitations:

• Kirchhoff’s current law (KCL): KCL cannot be utilised to solve for currents in circuits with nonlinear components like diodes and transistors. This is due to the fact that non-linear components do not respect charge conservation.KCL cannot be utilised to solve for currents in non-steady-state circuits. This is due to the fact that steady state is the condition in which the currents and voltages in a circuit do not change over time. Currents and voltages are continually fluctuating in a non-steady state, and KCL cannot reliably anticipate their values.
• Kirchhoff’s voltage law (KVL):KVL cannot be utilised to solve for voltages in circuits with nonlinear components like diodes and transistors. This is due to the fact that non-linear components do not follow the law of conservation of energy.
  KVL cannot be utilised to solve for voltages in non-steady-state circuits. This is due to the fact that steady state is the condition in which the currents and voltages in a circuit do not change over time. Currents and voltages are continually changing in a non-steady state, and KVL cannot reliably anticipate their values.

Kirchhoff’s Laws Equations

Kirchhoff’s laws are fundamental principles in electrical circuit theory, named after the German physicist Gustav Kirchhoff. They help analyze and solve electrical circuits by applying the principles of conservation of charge and energy. There are two main laws: Kirchhoff’s current law (KCL) and Kirchhoff’s voltage law (KVL). Here are the equations for each law:

1. Kirchhoff’s Current Law (KCL): KCL states that the algebraic sum of currents at any node (junction) in an electrical circuit is equal to zero. In other words, the total current flowing into a node is equal to the total current flowing out of the node.

The equation for KCL can be expressed as: ∑(I_in) = ∑(I_out)

Here, ∑(I_in) represents the sum of all currents flowing into the node, and ∑(I_out) represents the sum of all currents flowing out of the node.

2. Kirchhoff’s Voltage Law (KVL): KVL states that the sum of all the voltage drops around any closed loop in a circuit is equal to zero. In other words, the sum of the electromotive forces (EMFs) and the voltage drops across all the circuit elements in a closed loop is zero.

The equation for KVL can be expressed as: ∑(V_loop) = 0

Here, ∑(V_loop) represents the sum of all voltage drops (including the EMFs of voltage sources) encountered while traversing the closed loop.

These laws are crucial for analyzing complex electrical circuits, including circuits with multiple resistors, voltage sources, and current sources. By applying KCL and KVL, you can formulate and solve systems of equations to determine currents and voltages in a circuit.

Kirchhoff’s Laws Examples in Real Life

Kirchhoff’s laws have numerous real-life applications in various electrical systems and devices. Let’s explore a few practical examples where Kirchhoff’s laws are used:

1. Electric Circuits in Buildings: In residential and commercial buildings, electrical circuits are designed using Kirchhoff’s laws. For instance, when wiring a room with multiple electrical appliances and lights, electricians apply KCL and KVL to ensure that the currents and voltages at different points in the circuit comply with safety standards and meet the power requirements.
2. Electronics and Printed Circuit Boards (PCBs): Kirchhoff’s laws are fundamental in analyzing and designing electronic circuits, including those on PCBs. Engineers use these laws to calculate current flow and voltage drops through components like resistors, capacitors, and integrated circuits to ensure proper functionality and avoid overheating or damage.
3. Power Distribution Networks: In large-scale power distribution systems, Kirchhoff’s laws help engineers optimize the flow of electricity and identify potential problems. By applying these laws, they can calculate current loads, voltage drops, and power losses at different nodes in the power grid, enabling efficient distribution and minimizing losses.
4. Electrical Vehicle (EV) Systems: The electrical systems of EVs rely on Kirchhoff’s laws for designing battery packs, control circuits, and charging systems. Engineers apply these laws to manage the flow of current, monitor battery voltages, and ensure efficient power transfer between various components.
5. Circuit Analysis in Electronics Manufacturing: In the electronics manufacturing industry, Kirchhoff’s laws are used to analyze and troubleshoot circuit boards during quality control and testing processes. These laws help identify faulty components, short circuits, or open circuits that may impact the overall performance of the device.
6. Network Analysis in Telecommunications: In telecommunication networks, Kirchhoff’s laws are employed to analyze signal propagation, transmission losses, and power distribution in cables and network nodes. By applying these laws, engineers can optimize network performance and minimize signal degradation.
7. Biomedical Applications: In medical devices and equipment, such as electrocardiograms (ECGs) or electrical stimulators, Kirchhoff’s laws are used to understand and control electrical signals in the body. These laws help ensure that medical devices deliver the correct current and voltage levels safely and accurately.

These are just a few examples of how Kirchhoff’s laws are applied in real-life scenarios. Whether in simple electrical circuits or complex systems, Kirchhoff’s laws remain essential tools for electrical engineers, scientists, and technicians to understand and analyze electrical phenomena and ensure the efficient and safe operation of various electrical devices and systems.

Sharing is caring!