Mixed Fraction – Definition, Formula, Examples

Mixed Fraction is one of the most important types of fractions in Mathematics. The other two types of fractions are proper fractions and improper fractions. It is a unique type of fraction and one can easily recognize it by looking at its structure. It is made up of two different components. Let us explore the world of this unique fraction type by going through its different characteristics.

Mixed Fraction

As stated above, a mixed fraction consists of two components: a whole number and a fraction part. It is to be noted that the fraction part is always a proper fraction. It is also known by the name mixed numbers. So, simply put, the fractional part and a whole number part, when combined together forms a mixed fraction. For example,

$3\frac{4}{7}$

. Here 3 is the whole number part while

$\frac{4}{7}$

is the fractional part. But before learning different concepts related to a mixed fraction, let us recall the definition and terms related to fractions.

What is a Fraction?

A fraction is used to express a portion of a whole or a ratio of two values. The numerator and the denominator are its two component parts. The number above the fraction line is the numerator, which represents a portion of the whole, and the number below the fraction line is the denominator, which represents the total number of equally-sized pieces into which the whole is divided.

For example, in

$\frac{8}{13}$

, 8 is the numerator while 13 is the denominator.

Mixed Fraction Definition

Mixed fraction is a fraction in which there is a whole number component and and a fraction component. It is formed by joining a whole number and a fraction part. It is to be noted that the fraction part of a mixed number is always a proper fraction (numerator is always smaller than the denominator in a proper fraction). The mixed fraction can be better understood by the diagram given below:

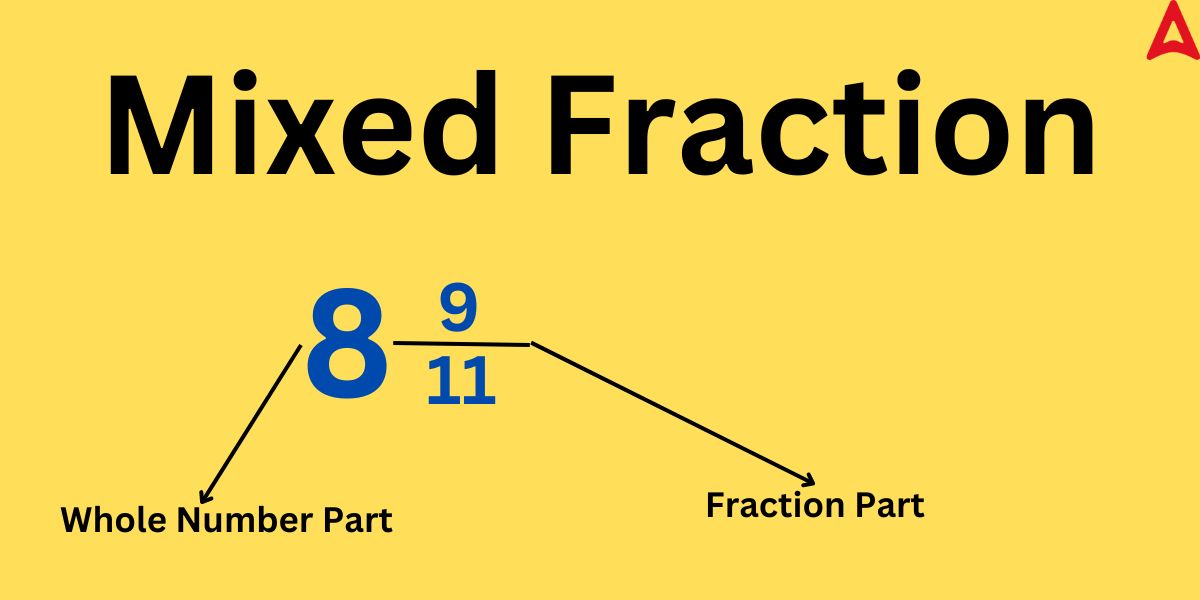
From the above diagram, we can observe that a mixed fraction consist of whole number part and a proper fraction part. The whole number part is actually the quotient f the improper fraction when divided to form the mixed number. The numerator of the fraction part is the remainder while the denominator is divisor.

Mixed Fraction Examples

Some of the examples of the mixed numbers are given below:

$4\frac{7}{8}, 11\frac{12}{18}, 9\frac{2}{7}, –18\frac{4}{13}, 9\frac{9}{10}, 12\frac{7}{15}$

, etc.

Mixed Fraction Formula

We can calculate the mixed number of a fraction by using the formula. The mixed number can be obtained from improper fraction by dividing the numerator by denominator. The conversion formula can be expressed as:

Mixed Number/Fraction =

$Quotient\frac{Remainder}{Divisor}$

where, Quotient = whole number part of the mixed number

Remainder = numerator of the fractional part

Divisor = denominator of improper fraction = denominator of the fractional part of the mixed number

Improper Fraction to Mixed Fraction Conversion

We can convert any improper fraction into a mixed number. Improper fractions are those fractions whose numerator is always greater than its denominator. We can convert the improper fraction to a mixed number by using the following conversion formula:

Mixed Number/Fraction =

$Quotient\frac{Remainder}{Divisor}$

where, Quotient = result obtained by dividing the numerator of the improper fraction by its denominator

Remainder = numerator of the fractional part of the mixed fraction

Divisor = denominator of improper fraction = denominator of the fractional part of the mixed number

This concept is explained through a diagram given below.

As we can observe from the above diagram, by doing a simple division process, we can convert an improper fraction into a mixed number.

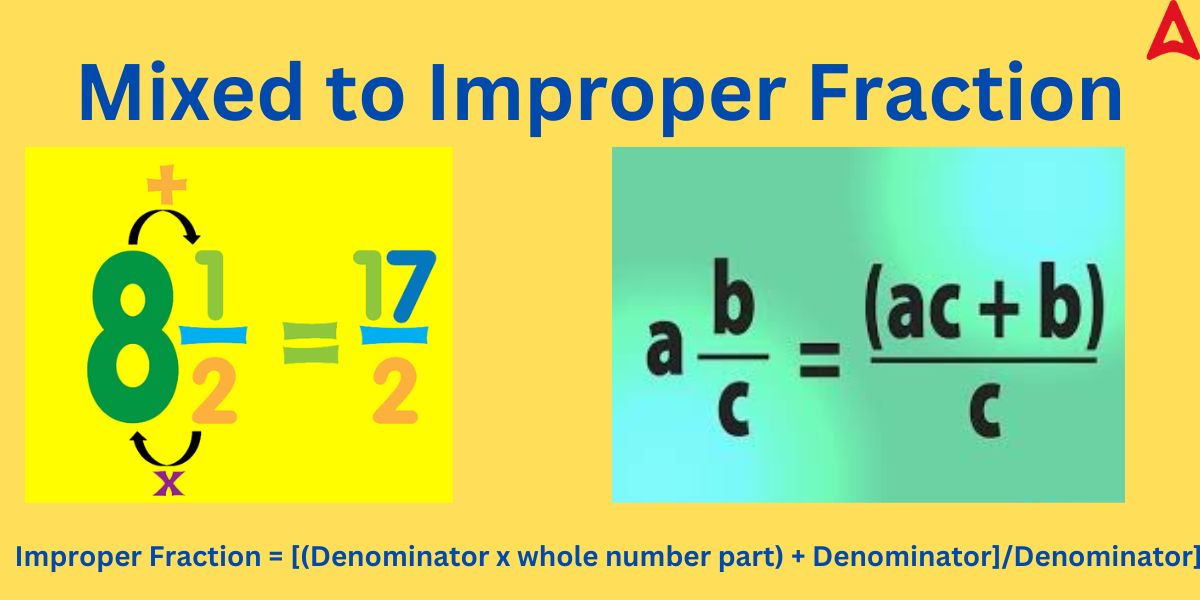
Mixed Fraction to Improper Fraction Conversion

The conversion mixed number into an improper fraction is the opposite of the above method. Let us understand this conversion through an example.

Let the mixed number be given as

$a\frac{b}{c}$

, then we can convert this number into an improper fraction by applying the rule:

(a. c + b)/c

For example,

$7\frac{4}{5}$

= ((7 x 5) + 4)/5 = 39/4

So, the general conversion rule from mixed number to improper fraction becomes:

Improper Fraction = [(Denominator x whole number part) + Denominator]/Denominator]

Addition of Mixed Fraction

We can perform the addition of two mixed numbers by following the steps mentioned below:

Step 1: Convert the given mixed numbers into improper fractions

Step 2: If the denominators of both fractions are same, then add numerators

Step 3: If denominators are different, then take LCM of the denominators of improper fractions

Step 4: Denominators and numerators of both fractions should be multiplied by a number so that their new denominator is the obtained LCM.

Step 5: Add the numerators by keeping the common denominator same

Step 6: Reduce the obtained result, if possible

Step 7: If the resulting fraction is improper, then convert it again into a mixed number

Subtraction of Mixed Fraction

Just like addition, two mixed fractions can be subtracted from one another. The steps for the same is given below:

Step 1: Convert the given mixed numbers into improper fractions

Step 2: If the denominators of both fractions are same, then subtract numerators

Step 3: If denominators are different, then take LCM of the denominators of improper fractions

Step 4: Denominators and numerators of both fractions should be multiplied by a number so that their new denominator is the obtained LCM.

Step 5: Subtract the numerators by keeping the common denominator same

Step 6: Reduce the obtained result, if possible

Step 7: If the resulting fraction is improper, then convert it again into a mixed number

Multiplication of Mixed Fraction

Two mixed numbers can be multiplied just like any other fractions. We can multiply mixed numbers using the following steps.

Step 1: Convert the given mixed numbers into improper fractions

Step 2: Multiply the numerator with numerator part and denominator with the denominator part.

Step 3: Reduce the fraction if possible

Step 4: If the resulting fraction is improper, then convert it again into a mixed number

Division of Mixed Fraction

Division of mixed number is an important concept. It is the reverse of multiplication. One can perform the division operation on mixed numbers by following the steps outlined below.

Step 1: Convert the given mixed numbers into improper fractions

Step 2: Convert the division sign into multiplication by reciprocating the improper fraction following the operator

Step 3: Multiply the numerator with numerator part and denominator with the denominator part.

Step 4: Reduce the fraction if possible

Step 5: If the resulting fraction is improper, then convert it again into a mixed number

Mixed Fraction Properties

Mixed numbers/fractions show many unique properties. Some of these properties are given below:

• A mixed number always contains a whole number part and a fraction part
• The fraction part of a mixed number is always a proper fraction
• Only improper fraction can be converted into mixed numbers

Mixed Fraction Solved Examples

Some of the solved examples on this topic is given below for students. By going through these solved questions, students will have a better idea of this important concept.

Example 1: Convert 

$3\frac{4}{5}$

into improper fraction.

Solution: given,

$3\frac{4}{5}$

so, improper fraction = ((5 x 3) + 4)/5

= 19/5

Example 2: Convert 11/4 into a mixed number.

Solution: Given 11/4

on dividing 11 by 4, we get

quotient = 2

remainder = 3

so, the mixed number =

$2\frac{3}{4}$

Example 3: Add 

$6\frac{3}{4} and 2\frac{1}{2}$

 

Solution: Given: 

$6\frac{3}{4} and 2\frac{1}{2}$

 

we have to find

$6\frac{3}{4} + 2\frac{1}{2}$

 

Converting the given fractions into improper fractions, we get

27/4 + 5/2

As the denominator are different, so we take the LCM of denominators

LCM of 4 and 2 = 4

so, changing the above fractions’ denominators equal to the obtained LCM, we get:

27/4 + 10/4

adding numerators, we get 37/4

converting again into mixed numbers, we obtain:

$9\frac{1}{4}$

is the desired answer

Example 4: Find the value of

$6\frac{3}{4} – 2\frac{1}{2}$

 

Solution: Given  

$6\frac{3}{4} and 2\frac{1}{2}$

 

we have to find 

$6\frac{3}{4} – 2\frac{1}{2}$

 

Converting the given fractions into improper fractions, we get

27/4 – 5/2

As the denominator are different, so we take the LCM of denominators

LCM of 4 and 2 = 4

so, changing the above fractions’ denominators equal to the obtained LCM, we get:

27/4 – 10/4

subtracting numerators, we get 17/4

converting again into mixed numbers, we obtain:

$4\frac{1}{4}$

is the desired answer

Example 5: Compute the value of  

$6\frac{3}{4} \times 2\frac{1}{2}$

 

Solution: Given:

 

$6\frac{3}{4} \times 2\frac{1}{2}$

 

on converting the above fractions into improper fractions, we get

27/4 x 5/4

on multiplying numerator by numerator and denominator by denominator, we get:

135/16

Converting the obtained result back into a mixed number, we get:

8

$\frac{7}{16}$

Example 6: Solve the fraction 

$6\frac{3}{4} ÷ 2\frac{1}{2}$

 

Solution: Given:

$6\frac{3}{4}÷ 2\frac{1}{2}$

 

on converting the above fractions into improper fractions, we get

27/4 ÷ 5/4

we will convert the divide sign into multiplication sign by reciprocating the number following the sign

So, 27/4 x 4/5

on multiplying numerator by numerator and denominator by denominator, we get:

27/5

Converting the obtained result back into a mixed number, we get:

$5\frac{2}{5}$

is the desired answer

Sharing is caring!