Sin 0 Value
Sin 0 is equal to 0 but the question is why the value of Sin 0 is zero.
Sin 0
Sin 0= 0. To clear this concept we have provided detailed information about Sin 0. The sine function shows a relation between perpendicular and hypotenuse. In triangle where one side makes an angle of 90 degrees is known as a right-angle triangle. The side in front of the 90-degree angle is called as hypotenuse side. Sin theta is equal to the perpendicular ratio hypotenuse of a right-angle triangle.
Check: Cos 60 Degrees Value
Sin 0 Degrees Value is equal to 0
Consider the ABC right-angle triangle, which has three sides: Base, Perpendicular, and hypotenuse. In a right-angled triangle, the three sides are usually referred to by their relation with the angle. The following are the three sides of a right-angled triangle:
- The longest side of the triangle is the hypotenuse, which is opposite to the right angle.
- Perpendicular in the right angle triangle is a side that makes a right angle with the Base.
- Base in the right-angle triangle is a side that adjoins the 90-degree angle.
Sin θ = Perpendicular/Hypotenues
Now, if we wish to calculate the value of sin 0 degrees, we must examine the coordinates points on the x and y plane. Since Sin 0 lies in the first coordinate and in the first coordinate the value of the x coordinate is 1 and the value of the y coordinate is 0, i.e. (x,y) is (1,0). That is, the perpendicular has a value of 0 and the hypotenuse has a value of 1. If we put these values in the sin theta equal to the ratio of perpendicular and hypotenuse let us see what will be the resultant.
Sin θ = Perpendicular/Hypotenues
θ = 0 degrees
Sin 0 = 0/1
Sin 0 = 0
If we divide 1 by zero we still get 0. Hence, the value of Sin 0 is zero. Let us know the values of sine for one complete revolution.
Sin All Degrees Value from 0° to 360°
Check the table given below to know the values of sin for 0 degrees to 360 degrees, i.e. one revolution.
| Sine Degrees | Values |
| Sin 0° | 0 |
| Sin 30° | 1/2 |
| Sin 45° | 1/√2 |
| Sin 60° | √3/2 |
| Sin 90° | 1 |
| Sin 180° | 0 |
| Sin 270° | -1 |
| Sin 360° | 0 |
Thus we have calculated the value of Sin 0, and we have mentioned other values of sin for different angles.
Sine 0 Degrees Value Based Examples
Maths is all about practice, students studying maths concepts should practice as much as questions they can. Here we have given the questions related to the sine function. The students must try to solve these questions without looking at the solutions, if unable to get answers then see answers and practice all the previous year and questions given in the textbook to have good command over trigonometry.
Example 1: Find the value of Sin 45 + Sin 45
Solution: As we know, the value of Sin 45 is 1/√2
Therefore, Sin 45 + Sin 45 = 1/√2 + 1/√2 = 2/√2 = √2
The answer of Sin 45 + Sin 45 is √2
Example 2: Find the value of Sin 360 +2 sin 30
Solution: As we know, the value of Sin 360 = 0, Sin 30 = 1/2
Therefore, Sin 360+2 Sin 30 = 0+2*(1/2) = 1
The answer of Sin 360 +2 sin 30 is 1.
Example 3: Find the value of 2Sin 90 +2 sin 30
Solution: As we know, the value of Sin 90 = 1, Sin 30 = 1/2
Therefore, 2Sin 90+2 Sin 30 = 1*2+2*(1/2) = 2+1 = 3
The answer of 2Sin 90 +2 Sin 30 is 3.
Example 4: Find the value of Sin 30 +2 sin 90
Solution: As we know, the value of Sin 90 = 1, Sin 30 = 1/2
Therefore, Sin 30+2 Sin 90 = ½ + 2*1 = 5/2
The answer of Sin 30 +2 sin 90 is 5/2
Example 5: Find the value of 10Sin 180 +2 sin 0
Solution: As we know, the value of Sin 180 = 0, Sin 0 = 0
Therefore, 10Sin 180 +2 sin 0 = 10*0+2*0 = 0
The answer of 10Sin 180 +2 sin 0 is 0.
Example 6: Find the value of 2Sin 90/2 sin 30
Solution: As we know, the value of Sin 90 = 1, Sin 30 = 1/2
Therefore, 2Sin 90/2 Sin 30 = 1/(1/2) = 1/2
The answer of 2Sin 90/2 sin 30 is 1/2.
Example 7: Find the value of 10 sin 270+ 20 sin 90
Solution: As we know, the value of Sin 90 = 1, Sin 270 = -1
Therefore, 10 sin 270+ 20 sin 90 = 10 * (-1) + 20*1 = 10
The answer of 10 sin 270+ 20 sin 90 is 10.

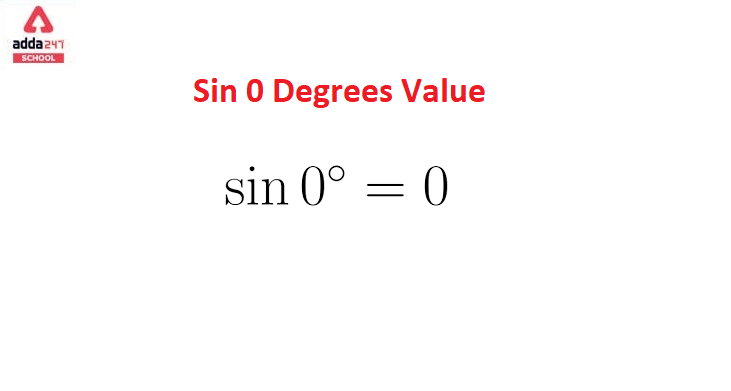







 CUET PG 2026 Registration Form OUT at ex...
CUET PG 2026 Registration Form OUT at ex...
 AILET Result 2026 Release Date, How to D...
AILET Result 2026 Release Date, How to D...
 CLAT Result 2026 Out, Download Scorecard...
CLAT Result 2026 Out, Download Scorecard...














