Sphere Formula For Diameter, Surface Area and Volume

The sphere Formula is very useful in geometry. In geometry, a sphere is described as a geometrical circular object in a 3 three-dimensional plane that has an absolute symmetrical shape. In childhood, we all are used to playing with cricket balls. So, a good example of a sphere is a cricket ball. In geometry, Sphere is a circular shape in a three-dimensional plane. In this article, we will learn about the sphere formula for determining its volume and total surface area.

What is a Sphere?

A sphere is described as a geometrical circular object in a 3 three-dimensional plane that has an absolute symmetrical shape. All the points  on the surface are present at an equal distance from the center (radius)
Example-Football, tennis ball, globe, etc.

Sphere Formula

The formulas for a sphere are as follows:

1. Surface Area of a Sphere:

   The surface area (A) of a sphere with radius (r) is given by:

   Surface Area (A) = 4πr²

   Where:

   • π (pi) is a constant approximately equal to 3.14159.
   • r is the radius of the sphere.
2. Volume of a Sphere:

   The volume (V) of a sphere with radius (r) is given by:

   Volume (V) = (4/3)πr³

   Where:

   • π (pi) is the same constant.
   • r is the radius of the sphere.

These formulas allow you to calculate the surface area and volume of a sphere based on its radius. Keep in mind that these formulas are specific to three-dimensional spheres and assume a perfect, mathematically defined shape.

Sphere All Formula List

list of formulas related to spheres:

1. Surface Area of a Sphere:

   The surface area (A) of a sphere with radius (r) is given by:

   Surface Area (A) = 4πr²

   Where:

   • π (pi) is a constant approximately equal to 3.14159.
   • r is the radius of the sphere.
2. Volume of a Sphere:

   The volume (V) of a sphere with radius (r) is given by:

   Volume (V) = (4/3)πr³

   Where:

   • π (pi) is the same constant.
   • r is the radius of the sphere.
3. Diameter of a Sphere:

   The diameter (d) of a sphere is twice the radius:

   Diameter (d) = 2r

4. Circumference of a Great Circle on the Sphere:

   The circumference (C) of a great circle on a sphere with radius (r) is given by:

   Circumference (C) = 2πr

   Where:

   • π (pi) is the constant approximately equal to 3.14159.
   • r is the radius of the sphere.
5. Distance between Two Points on the Sphere:

   The distance (d) between two points A and B on the surface of a sphere with radii r1 and r2 (along the radii) and subtending an angle θ between them is given by the spherical law of cosines:

   Distance (d) = sqrt(r1² + r2² – 2 * r1 * r2 * cos(θ))

6. Spherical Sector Volume:

   The volume (V) of a spherical sector (a portion of a sphere enclosed by two radii and a cone) is given by:

   Volume (V) = (1/6)πh(3a² + h²)

   Where:

   • π (pi) is the constant approximately equal to 3.14159.
   • h is the height of the sector (distance along the curved surface from the apex to the base).
   • a is the radius of the base of the sector.

These are some of the key formulas related to spheres. They can be used to calculate various properties of spheres and solve problems involving spheres in geometry and physics.

Sphere formula Total Surface Area (TSA) properties

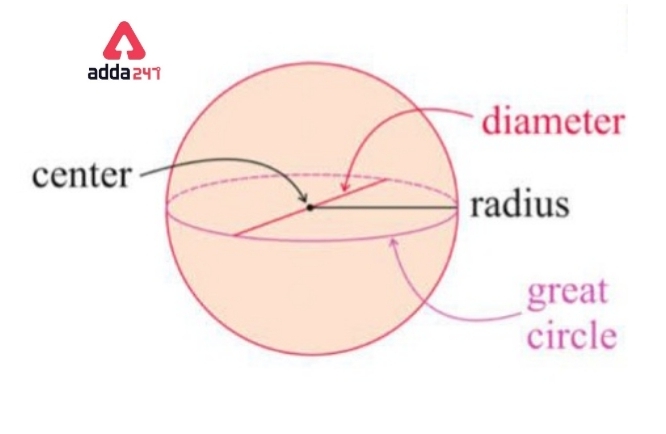
Center of the sphere-In a sphere all the points on the surface are present at the same distance from a fixed point, the point is regarded as the Center of the sphere.

The radius of the sphere-A straight line which forms a connection between the center of the sphere and any point present on the surface. is known as the radius. Generally, Radius is denoted by the alphabet letter r.

Diameter of a sphere- Diameter is the longest straight line that passes through the center of the sphere and meets any two different points present on the surface of the sphere. Thus. Those two points and the center of the sphere lie in diameter, denoted by D.
In a sphere, the Diameter is always doubled in the radius in length.

Sphere formula of Area, Diameter, Volume

Sphere Diameter Formula

Diameter is the longest straight line that passes through the center of the sphere and meets any two different points present on the surface of the sphere. A sphere’s diameter is always doubled because of the radius in length in that particular sphere.
D = 2 r

Sphere Area Formula

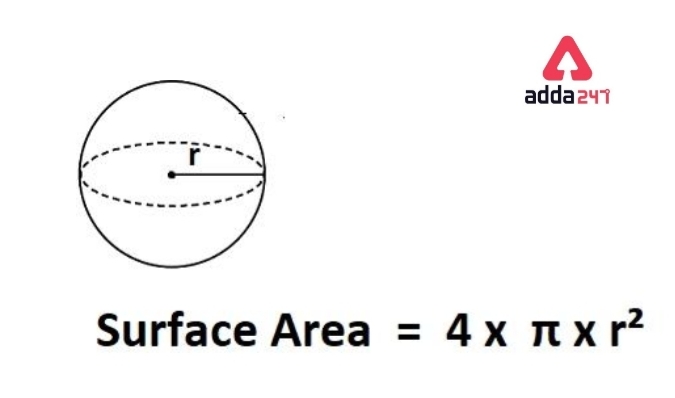
The total surface area of a sphere is considered as its total curved surface. The sphere does not have any edges or any lateral surfaces. So, we consider that the total surface area of the sphere equals the total curved surface area.
The formula for determining the total surface area of a sphere is,
Total surface area  = 4 π r² square units.
{ In above, π is a constant value which is equal to 3.14 or 22/7 }

Sphere Volume Formula

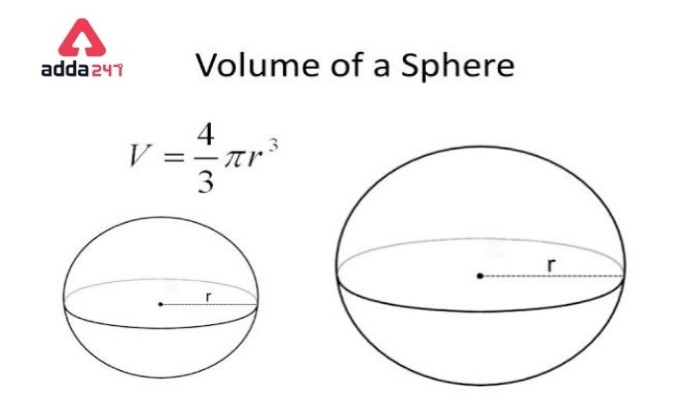
The volume of a Sphere defines as the holding capacity of the sphere into it. The formula for determining the volume of a sphere is –
Let’s assume V is the volume of the sphere,
Then, Volume = 4/3 π r³  cubic units, in which π is a constant that equals 3.14 or 22/7, and r is the radius of the sphere.

Sphere formula: Difference between Circle and Sphere Explanation

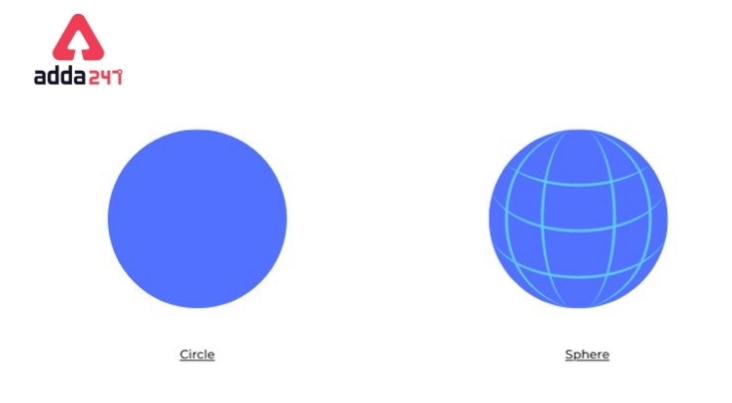
Although the shape of both figures is circular, the main difference between Circle and a sphere is,  Circle is a two-dimensional figure, on the other hand, a sphere is a three-dimensional object. A sphere has area and volume. But a circle only has its area and circumference.

Sphere Formula Examples

Q. Diameter of a sphere is 12 cm . Find the Radius and total surface area of the sphere.
a) 6 cm and 270 πcm² b) 6 cm and 144 π cm² c)  12 cm and 144 π cm²  d) None of these. 
Answer-Let’s suppose the radius of the sphere is r
The diameter of the given sphere is -D= 12 cm.
We all know that Diameter is doubled in radius in length.
So, D= 2r
or, 12 = 2r
or, r = 6 cm

The formula for the total surface area of a sphere is –
4 π r² square units.
Total surface area= 4 π (6)²
= 4× π ×36
= 144 π or 452.16 cm²

Q. Find the volume of a sphere which have a radius of   3 cm.
a) 27π cm³ b) 36π cm³ c)  36 cm³ d) None of those
Answer-
The formula for determining the volume of the sphere is-
V = 4/3 π r³  cubic units.

Volume- V=  4/3  π  ( 3) ³  cm³
V= 36 π  cm³

So, option ( b) is correct.

Q.If the Surface area of a sphere is 616 cm² . Find the radius of the sphere.
(a) 4  cm   (b) 7 cm (c)   49 cm (d) None of these.
Answer- we know that the formula for the surface area of as phere is – 4πr²
Here, the Surface area of the sphere is 616 cm².
4πr² = 616
r² = 616 /(4 × 22/7) [ π =22/7]
r² = 616 ×7 / 22×4
r² = 49
or, r = 7 cm
The radius of the sphere is 7 cm.

Hence, option (b)is correct.

Q. If the radius of a sphere is increased 2 times. What is its volume? (Radius = r)
(a) 4/3 πr³  (b)43/3πr³  (c)  32/3 r³ (d) None of these.
Answer – The previous radius of the  sphere is  r
After increasing 2 times, the radius is  2r

The volume of the sphere is – 4/3 π(r)³
= 4/3 π(2r)³ = 4/3 π(8r³ ) = 32/3 r³ cubic units .

Hence, option (c)is correct.

Sphere Formula Practice questions

1. If the radius of a sphere is increased 2 times. What is its total surface? (Radius = r)
2. The diameter of a sphere is 6 cm. Find the Radius and total surface area of the sphere.
3. Find the volume of a sphere which have a radius of   5 cm.
4. If the Surface area of a sphere is 343 cm³. Calculate the diameter of the sphere.

Formula of Sphere QNAs

Q. Is the sphere three-dimensional?
Answer- Yes. The sphere is a three-dimensional circular figure.

Q. What is a Sphere?
Answer- A sphere is described as a geometrical circular figure in a 3 three-dimensional plane that has an absolute symmetrical shape.
Example-football ,cricket ball ,globe etc.

Q. How to calculate the volume of a sphere?
Answer- The formula for  calculating the  volume of a sphere is
V = 4/3 π r³  cubic units, in which  π is a constant that equals 3.14 or 22/7,r is the radius of the sphere

Q. How to find the surface area of a sphere?
Answer-  The total surface area of a sphere is considered as its total curved surface.
The formula for determining the total surface area of a sphere is – = 4 π r² square units.

Q. What is the difference between Circle and a sphere?
Answer- Although the shape of both figures is similar, the main difference between Circle and a sphere is  Circle is two-dimensional, on the other hand, the sphere is a three-dimensional figure.

Sharing is caring!