What is 72 formula of trigonometry?

We can represent cos 72 degrees using trigonometry as: ± √(1-sin²(72°)) ± 1/√(1 + tan²(72°)) ± cot 72°/√(1 + cot²(72°)).

What is the basic formula of trigonometry for Class 9?

Sin = y/1 = y, cos = x/1 = x, tan = y/x are the basic trigonometric function formulas for the Unit Circle.

What are the 12 trigonometric identities?

All 12 trigonometric identities are discussed in this article in detail.

What is tan 70 formula?

Tan 70 degrees has a value of 2.7474774. Tan 70 degrees is expressed as tan (70° /180°), i.e., tan (7/18) or tan (1.221730...).

Trigonometry Formulas for Class 11 and 12 PDF Download

Q: What are the basic formulas for trigonometry?

the formulas for fundamental trigonometric functions are - sin θ = Opposite Side/Hypotenuse. cos θ = Adjacent Side/Hypotenuse. tan θ = Opposite Side/Adjacent Side. sec θ = Hypotenuse/Adjacent Side. cosec θ = Hypotenuse/Opposite Side. cot θ = Adjacent Side/Opposite Side.

Table of Contents

The formulas of Trigonometry are one of the most significant formulas to study in Class 9, 10, 11, and 12. When taking any national-level competitive exam, trigonometry is an important part of the Quantitative Aptitude section. Trigonometry is the study of triangles, with trigon meaning triangle and metry meaning measurement.

Trigonometry is a discipline of mathematics concerned with the angles and lengths of a triangle with a right angle. Read the full article to know the all necessary Trigonometry Formulas for Class 10, 11, and 12 and it will immensely help in your study.

Trigonometry Formula

Trigonometry is a most important topic of Maths that will help us to understand the relationships between the angles and sides of triangles and Trigonometry formulas give us the facility to solve complex problems involving angles, distances, and other geometric concepts. This article on Formulas of Trigonometry includes a trigonometry table with function values and all formulas of the Trigonometry concept which is useful in board exams.

We normally study fundamental trigonometry in classes 9 and 10, but in trigonometry classes 12 and 11, we study trigonometry that has applications in astronomy, engineering, architectural design, and physics.

Trigonometry Formulas Origin

A list of trigonometric formulas has been developed having relation to a right-angled triangle. There are six trigonometric functions: Sin, Cos, Tan, Sec, Cosec, and Cot. Trigonometric ratios can be used to calculate the current lengths and angles. All formulas of trigonometry for class 10, trigonometry tricks, and trigonometry questions revolve around these six functions.

Formation of Trigonometry Ratios

Let us first look at how the basic formulas for the six trigonometric functions Sin, Cos, Tan, Sec, Cosec, and Cot are produced. We’re looking at a right-angled triangle (as shown in the image below), which has an angle, a hypotenuse, a side opposite the angle, and a side next to the angle.

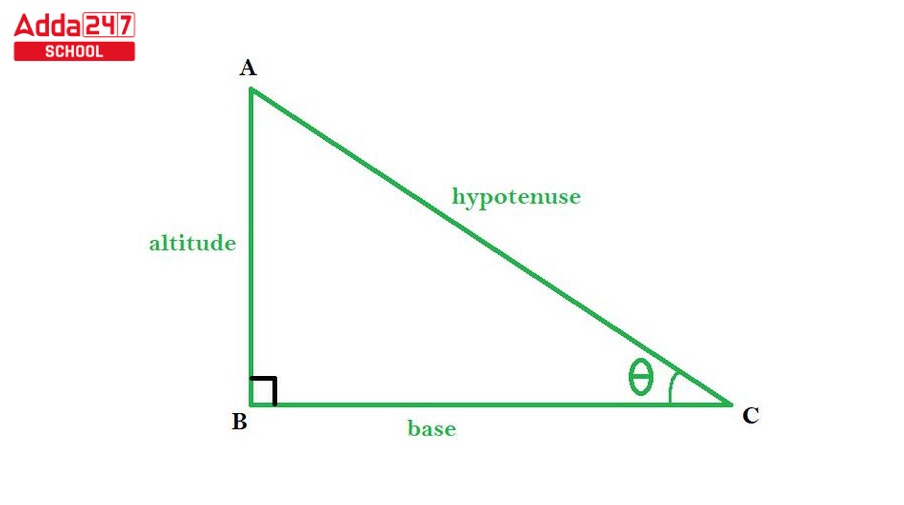
Trigonometric Ratios
sin θ = Opposite side / Hypotenuse	sec θ = Hypotenuse / Adjacent side
cos θ = Adjacent Side / Hypotenuse	cosec θ = Hypotenuse / Opposite side
tan θ = Opposite side / Adjacent Side	cot θ = Adjacent side / Opposite side

Trigonometric Formula Ratios In Other Words

Trigonometry ratios relate angles and sides in triangles in Trigonometry. Sine (sin) is opposite/hypotenuse, cosine (cos) is adjacent/hypotenuse, and tangent (tan) is opposite/adjacent. These trigonometric ratios help us to solve triangle problems and model world phenomena in various fields, like space, physics, and engineering.

sinθ = Opposite Side / Hypotenuse
cosθ = Adjacent Side / Hypotenuse
tanθ = Opposite Side / Adjacent Side
secθ = Hypotenuse / Adjacent Side
cosecθ = Hypotenuse / Opposite Side
cotθ = Adjacent Side / Opposite Side.

Trigonometry Formula in Degrees

The identities and ratios serve as the foundation for all formulas in trigonometry. Trigonometry ratios are used to create the relationship between triangle angles and side lengths. It is made up of trigonometric ratios such as sine, cosine, tangent, cosecant, secant, and cotangent.

These ratios can be expressed as sin, cos, tan, cosec, sec, and cot in a trigonometry table. The trigonometric ratios values can be used to calculate the values of trigonometric standard angles such as 0°, 30°, 45°, 60°, and 90°. The formulas and values of the trigonometric ratios are shown below.

Trigonometric Ratios Value
Degrees (°)	Sine (sin)	Cosine (cos)	Tangent (tan)	Cosecant (csc)	Secant (sec)	Cotangent (cot)
0°	0	1	0	undefined	1	undefined
30°	1/2	√3/2	√3/3	2√3/3	2	√3
45°	√2/2	√2/2	1	√2	√2	1
60°	√3/2	1/2	√3	2/√3	2	1/√3
90°	1	0	undefined	1	undefined	0
120°	√3/2	-1/2	-√3	-2/√3	-2	-1/√3
135°	√2/2	-√2/2	-1	-√2	-√2	-1
150°	1/2	-√3/2	-√3/3	-2√3/3	-2	-√3
180°	0	-1	0	undefined	-1	undefined
210°	-1/2	-√3/2	√3/3	-2√3/3	-2	√3
225°	-√2/2	-√2/2	1	-√2	-√2	1
240°	-√3/2	-1/2	√3	-2/√3	-2	1/√3
270°	-1	0	undefined	-1	undefined	0
300°	-√3/2	1/2	-√3	2/√3	2	-1/√3
315°	-√2/2	√2/2	-1	√2	√2	-1
330°	-1/2	√3/2	-√3/3	2√3/3	2	√3
360°	0	1	0	undefined	1	undefined

All Trigonometry Formulas List for Class 10, 11 and 12

Trigonometry formula Lists are mathematical statements that describe how the angles and sides of a right triangle are related. Every trigonometric formula is built on identities and ratios. Trigonometric concepts are used to construct the relationship between a triangle’s side and angle lengths. Consider the following sets of trigonometric formulas.

Even and Odd Angle Formulas
sin(-θ) = -sinθ	cosec(-θ) = -cosecθ
cos(-θ) = cosθ	sec(-θ) = secθ
tan(-θ) = -tanθ	cot(-θ) = -cotθ
Co-function Formulas
sin(900-θ) = cosθ	cosec(900-θ) = secθ
cos(900-θ) = sinθ	sec(900-θ) = cosecθ
tan(900-θ) = cotθ	cot(900-θ) = tanθ
Double Angle Formulas
sin2θ = 2 sinθcosθ
cos2θ = 1 – 2sin²θ
tan2θ = 2tanθ / 1- tan²θ
Thrice of Angle Formulas
sin2θ = 2 sinθ cosθ
cos2θ = 1 – 2sin²θ
tan2θ = 2tanθ / 1- tan²θ
sin3θ = 3sinθ – 4 sin³θ
Cos 3θ = 4cos³θ – 3 cosθ
Tan 3θ = 3tanθ – tan³θ / 1-3tan²θ
Cot 3θ = cot³θ-3cotθ / 3cot²θ-1
Half Angle Formulas
$\sin (θ) = \pm \sqrt{\frac{1 - \cos (2 θ)}{2}}$ $\cos (θ) = \pm \sqrt{\frac{1 + \cos (2 θ)}{2}}$ $\tan (θ) = \pm \sqrt{\frac{1 - \cos (2 θ)}{1 - \cos (2 θ)}}$

All Trigonometry Formulas for Class 12

For the right triangle, a set of trigonometric formulas was developed. A set of trigonometry-based formulas will assist students in swiftly solving trigonometry difficulties. A list of formulas in Trigonometry for class 12 based on the right triangle and the unit circle is provided below.

Trigonometric Sum and Difference Formulas

Sin (A+B) = Sin A Cos B + Cos A Sin B

Sin (A-B) = Sin A Cos B – Cos A Sin B

Cos (A+B) = Cos A Cos B – Sin A Sin B

Cos (A-B) = Cos A Cos B + Sin A Sin B

Tan (A+B) = Tan A + Tan B / 1 – TanATanB

Tan (A-B) = Tan A – Tan B / 1 + TanATanB

Sum to Product Formulas

\sin (A) + \sin (B) = 2 \sin (\frac{A + B}{2}) \cos (\frac{A - B}{2})

\sin (A) - \sin (B) = 2 \cos (\frac{A + B}{2}) \sin (\frac{A - B}{2})

\cos (A) + \cos (B) = 2 \cos (\frac{A + B}{2}) \cos (\frac{A - B}{2})

\cos (A) - \cos (B) = 2 \sin () (\frac{A + B}{2}) \sin (\frac{A - B}{2})

Product to Sum Formulas

Sin A Sin B = ½ [Cos (A-B) – Cos (A+B)]

Cos A Cos B = ½ [Cos (A-B) + Cos (A+B)]

Sin A Cos B = ½ [Sin (A+B) + Sin (A-B)]

Cos A Sin B = ½ [Sin (A+B) – Sin (A-B)]

Inverse Trigonometric Functions

sin^-1(sin θ) = θ

cos^-1(cos θ) = θ

tan^-1(tan θ) = θ

Trigonometric Formulas for Circle

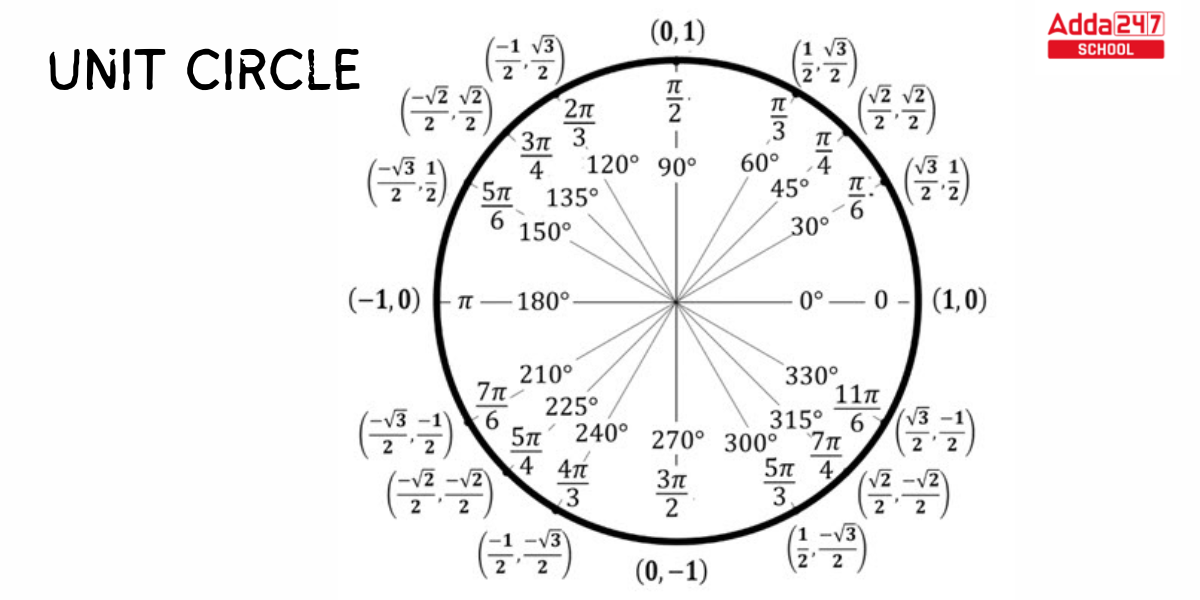
Unit Circle

The unit circle in trigonometry is the circle of radius 1 centered at the origin (0, 0) in the coordinate system known as Cartesian on the Euclidean plane. If (x, y) is a point on the circumference of the unit circle, then |x| and |y| are the lengths of the legs of a right triangle with a hypotenuse length of 1. Thus, x and y satisfy the equation according to the Pythagorean theorem, That is x² + y² = 1.

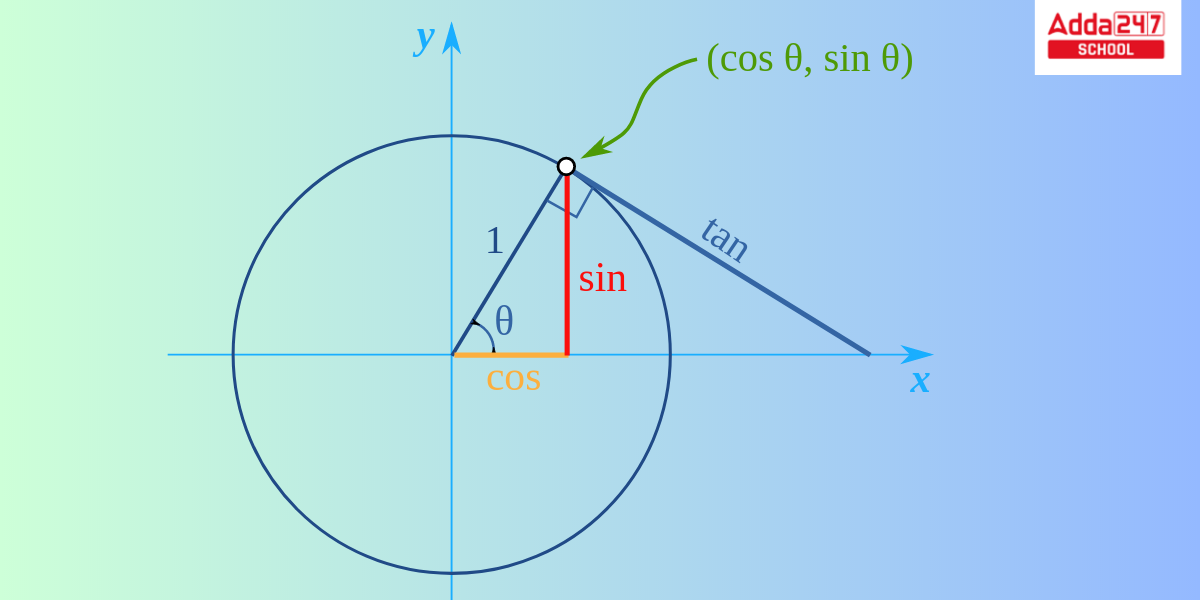
In the accompanying illustration, the center is placed on a graph where the x and y axes intersect, resulting in this elegant arrangement. We readily obtained the varied values of sin and cos ratios for angles of various degrees such as 0°, 30°, 45°, 60°, 90°, and so on in all four quadrants using the unit circle. Because it is so basic, it is an excellent way to learn and discuss lengths and angles using a unit circle.

Trigonometric Formula for Unit Circle

In a comparable manner to a unit circle, where the radius equals 1 and the angle is θ. The radius of the unit circle is equal to the value of the hypotenuse and neighboring side in this case. example – Hypotenuse = Adjacent side to θ = 1, As a result, the trigonometric formula for the unit circle are given by:

Trigonometric Formulas List: Ratios for Unit Circle
sin θ = y/1 = y	cot θ = x/y
cos θ = x/1 = x	sec θ = 1/x
tan θ = y/x	cosec θ = 1/y

Trigonometric Formulas for Complementary and Supplementary Angle

Complementary Angles: Pair of angles whose sum is equal to 90°
Supplementary Angles: Pair of angles whose sum is equal to 180°

Formula of Complementary Angles

Check here all conversions of (90° – θ).

sin (90° – θ) = cos θ

cos (90° – θ) = sin θ

tan (90° – θ) = cot θ

cot (90° – θ) = tan θ

sec (90° – θ) = cosec θ

cosec (90° – θ) = sec θ

Formula of Supplementary Angles

Check here all conversions of (180° – θ).

sin (180° – θ) = sin θ

cos (180° – θ) = – cos θ

tan (180° – θ) = – tan θ

cot (180° – θ) = – cot θ

sec (180° – θ) = – sec θ

cosec (180° – θ) = cosec θ

Trigonometry Identities

Trigonometric identities are equations involving trigonometric functions that hold true for all values of the variables involved. These identities are essential in simplifying expressions, solving equations, and proving other mathematical statements involving trigonometric functions. Here are some fundamental trigonometric identities:

Pythagorean Identities
Reciprocal Identities
Quotient Identities
Co-Function Identities
Even-Odd Identities
Double Angle Identities
Half Angle Identities
Sum and Difference Identities

These are just a selection of important trigonometric identities. Depending on the context, there are many more identities that can be useful for solving specific problems or simplifying expressions involving trigonometric functions.

Pythagorean Trigonometric Identities

The Pythagorean Theorem is a theorem describing the lengths of right triangle sides. It explains the link between the triangle’s three sides and shows how to determine one side given the lengths of the other two sides. The Pythagorean Theorem formula is – a² + b² = c²

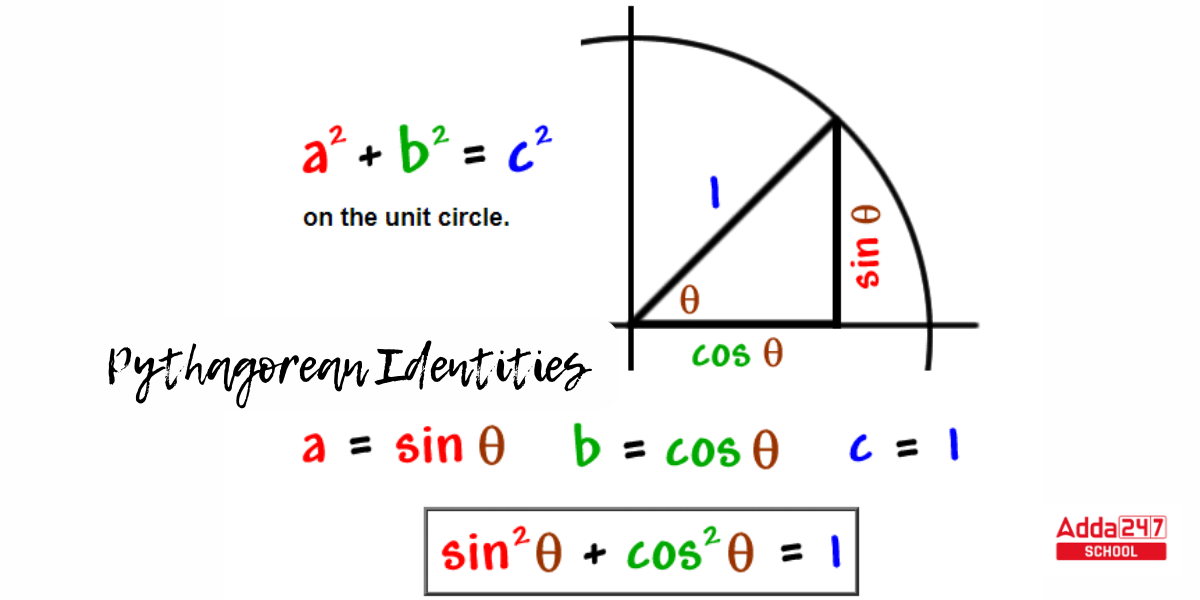
This is known as the Pythagorean Theorem identity. where c is the hypotenuse, or side opposing the right angle, and the other two sides, a and b, are referred to as the legs. The following are the most fundamental trigonometric identities employing the Pythagorean Theorem called Pythagorean Identities.

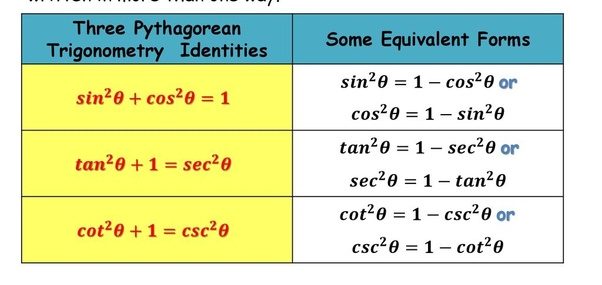
1. sin2 θ + cos2 θ = 1
2. tan2 θ + 1 = sec2 θ
3. 1 + cot2 θ = cosec2 θ

Reciprocal Trigonometric Identities

The reciprocals of all three standard functions of trigonometry, sine, cosine, and tangent, are known as reciprocal identities. Reciprocal identities are also known as inverse identities in trigonometry. Inverse sine, cosine, and tangent functions are expressed as “arc” prefixes such as arcsine, arccosine, and arctan.

Each fundamental trigonometric function is the inverse of another fundamental trigonometric function. For example, cosecant is the sine function’s reciprocal identity. The formulas for the six major reciprocal identities are as follows:

Trigonometric Reciprocal Identities
sinθ = 1/cosecθ	secθ = 1/cosθ
cosecθ = 1/sinθ	tanθ = 1/cotθ
cosθ = 1/secθ	cotθ = 1/tanθ

The sum of a trigonometric function and its reciprocal is one. As a result, there is

Relationship between Reciprocal Identities –

sin θ × cosec θ = 1
cos θ × sec θ = 1
tan θ × cot θ = 1

Quotient Trigonometric Identities

In right triangle trigonometry, there are two different quotient identities that can be employed.
A quotient identity defines the tangent and cotangent relations in terms of sine and cosine. Consider the sine, cosine, and tangent functions first. These functions are defined for angles of rotation (not necessarily in the unit circle) as follows:

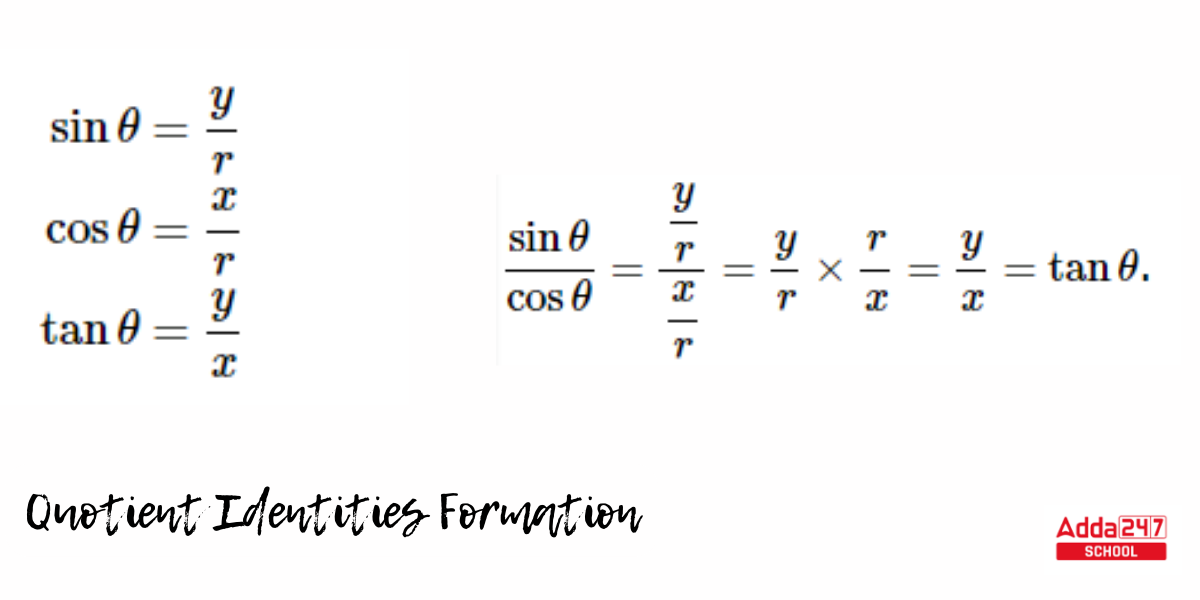
Given these definitions, we can demonstrate that tanθ=sinθ/cosθ as long as cosθ≠0. The equation tanθ=sinθ/cosθ is thus an identity that we can use to get the value of the tangent function given the sine and cosine values.

Co Function Trigonometric Identities

Cofunction identities are trigonometric identities that demonstrate the link between angles that are complementary and trigonometric functions/ratios such as sine and cosine, tangent and cotangent, secant and cosecant. The Co- Function Formulas are follow:

Co-function Formulas
sin(90º-θ) = cosθ	cosec(90º-θ) = secθ
cos(90º-θ) = sinθ	sec(90º-θ) = cosecθ
tan(90º-θ) = cotθ	cot(90º-θ) = tanθ

Even-Odd Trigonometric Identities

Even and odd identities for trigonometric functions entail using the evenness or oddness of the trig function to obtain the trig values of negative angles. Odd functions include sine, tangent, cosecant, and cotangent. The cosine and secant functions are both positive. The even and odd identities, like all trig identities, are important in physical sciences and engineering.

Even and Odd Angle Formulas
sin(-θ) = -sinθ	cosec(-θ) = -cosecθ
cos(-θ) = cosθ	sec(-θ) = secθ
tan(-θ) = -tanθ	cot(-θ) = -cotθ

Odd Identities

Odd identities are trigonometric identities that arise because a given trigonometric function is an odd function. Remember that an odd function is one that has the property f(-x) = – f(x). That is, the outputs of equivalent positive and negative inputs have the same absolute value. However, the indications of these outputs will differ.

Even Identities

In trigonometry, even identities are identities that arise from the fact that a given trig function is even. Remember that an even function is one in which f(-x) = f(x). That means, the output of comparable positive and negative inputs is the same. Reflecting such functions over the y-axis translates them to themselves since they are symmetric about the y-axis. Cosine and secant are two even trig functions. As a result, two trigonometric even identities exist:

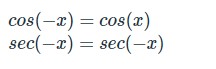Double Angle and Half Angle Trigonometric Identities

Double angle formulas are used to express trigonometric ratios of double angles (2θ) in terms of single angle trigonometric ratios (θ). The double angle formulae are special examples of (and consequently derived from) the trigonometric sum formulas, and several alternate formulas are generated by applying the Pythagorean identities.
The double angle formulas can be used to derive half-angle formulas. As we know, the angle sum and difference formulae of trigonometry can be used to generate the double angle formulas. In half angle formulas, half-angles are commonly indicated by /2, x/2, A/2, and so on, and the half-angle is a sub-multiple angle.

Double Angle Formulas
sin2θ = 2 sinθ cosθ
cos2θ = 1 – 2sin²θ
tan2θ = 2tanθ / 1- tan²θ

The half angle formulas are used to calculate the exact values of trigonometric ratios of angles for example 15° (half of the standard angle 30°), 22.5° (half of the typical angle 45°), and so on.

\sin (θ) = \pm \sqrt{\frac{1 - \cos (2 θ)}{2}}

\cos (θ) = \pm \sqrt{\frac{1 + \cos (2 θ)}{2}}

\tan (θ) = \pm \sqrt{\frac{1 - \cos (2 θ)}{1 - \cos (2 θ)}}

Sum and Difference Trigonometric Identities

Addition and Subtraction Trigonometric formulas are used to determine the values of trigonometric functions at any angle where the given angle can be expressed as the sum or difference of standard angles such as 0°, 30°, 45°, 60°, 90°, and 180°. To evaluate the cosine function at 15°, for example, we can express 15° as the difference between 45° and 30°; i.e., cos 15° = cos (45°-15°). In trigonometry, we mostly use 6 sum and difference formulas.

Trigonometric Sum and Difference Formulas

Sin (A+B) = Sin A Cos B + Cos A Sin B

Sin (A-B) = Sin A Cos B – Cos A Sin B

Cos (A+B) = Cos A Cos B – Sin A Sin B

Cos (A-B) = Cos A Cos B + Sin A Sin B

Tan (A+B) = Tan A + Tan B / 1 – TanATanB

Tan (A-B) = Tan A – Tan B / 1 + TanATanB

Trigonometry Identities Formulas List

As previously established, all formulas of Trigonometry are built on identities and ratios. The compilation of trigonometry formulas PDF class 10 will assist students in quickly solving trigonometric problems. The trigonometric ident table based on the right-angled triangle is provided below and can be used as a reference for studying trigonometry.

Trigonometric Reciprocal Identities
sinθ = 1/cosecθ	secθ = 1/cosθ
cosecθ = 1/sinθ	tanθ = 1/cotθ
cosθ = 1/secθ	cotθ = 1/tanθ
Tangent and Cotangent Identities / Quotient Identities
tan θ = sin θ / cos θ
cot θ = cos θ / sin θ
Pythagorean Identities
sin²θ + cos²θ = 1
1 + tan²θ = sec²θ
1 + cot²θ = cosec²θ

Trigonometric Functions Class 10

start learning about basic trigonometric functions and their ratios. Trigonometry deals with the relationships between the angles and sides of a right-angled triangle. The three primary trigonometric functions are Sine (sin), Cosine (cos), and Tangent (tan). Here’s an overview of these functions:

Sine (sin)

In a right-angled triangle, the sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse.
Mathematically, sin(A) = Opposite side / Hypotenuse

Cosine (cos):

The cosine of an angle in a right-angled triangle is the ratio of the length of the adjacent side to the length of the hypotenuse.

Mathematically, cos(A) = Adjacent side / Hypotenuse

Tangent (tan):

The tangent of an angle in a right-angled triangle is the ratio of the length of the side opposite the angle to the length of the adjacent side. Mathematically, tan(A) = Opposite side / Adjacent side

Additional functions that are introduced in later classes include Cosecant (cosec), Secant (sec), and Cotangent (cot). They are the reciprocals of sine, cosine, and tangent, respectively.

Cosecant (cosec):

cosec(A) = 1 / sin(A)

Secant (sec):
sec(A) = 1 / cos(A)

Cotangent (cot):
cot(A) = 1 / tan(A)

These trigonometric functions are fundamental in solving various problems related to heights and distances, angles of elevation and depression, and other real-world applications involving right-angled triangles.

Trigonometry All Formulas Based Solved Problems

Q.1: What is the value of (sin 30° + cos 30°) – (sin 60° + cos 60°)?

Solution:

Given,

(sin 30° + cos 30°) – (sin 60° + cos 60°)

= (½) + (√3/2) – (√3/2) – (½)

= 0

Q.2: If cos A = 4/5, then find the value of tan A.

Solution:

Given,

cos A = ⅘

As we know, from trigonometry identities,

1 + tan²A = sec²A

sec²A – 1 = tan²A

(1/cos²A) -1 = tan²A

Putting the value of cos A = ⅘.

(5/4)² – 1 = tan² A

(25 – 16)/16 = tan² A

tan²A = 9/16

tan A = 3/4

Trigonometric Formulas Based Practice Problems

If sin A = 1/2 then find the value of sin 2A.
Prove that tan θ + tan(90° – θ) = sec θ sec(90° – θ)
If Tan A = 3/4, the find sin A cos A.

All Trigonometry Formulas PDF

All Formulas present in Trigonometry for Class 11 and 12 PDF Download by Clicking on the below link

Trigonometry Formulas PDF

Links
Physics Formula	Algebra Formula
Integration Formula	Mensuration Formula
Time and Work Formula	Time and Distance Formula
Profit and Loss Formula	a3 b3 Formula