Volume of Hemisphere Formula, Definition, Examples

In geometry, we looked at various types of three-dimensional shapes. The hemisphere is a geometrical figure in three dimensions.

Volume of Hemisphere Definition

The volume of Hemisphere basically refers to a hemisphere’s capacity. Geometrically, a hemisphere is the exact half of a sphere. As a result, the volume of a hemisphere is half that of a sphere. In this essay, we will learn about the Volume of Hemisphere Formula, its derivation, and examples.

What is a Hemisphere?

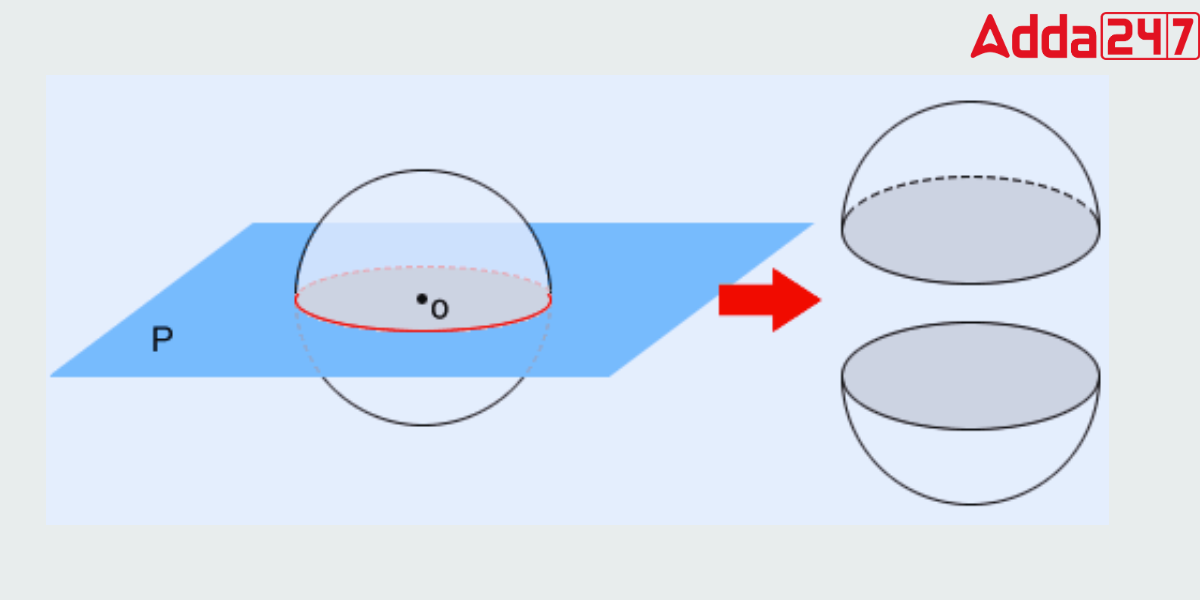
The prefix “hemi” comes from Greek and means “half.” As a result, a hemisphere merely refers to half of a spherical. A sphere is defined as a three-dimensional set of points, with all points on the surface being equidistant from the center. sphere. A hemisphere is a three-dimensional (3D) form that is half the size of a sphereThe shape formed when a sphere is cut by a plane traveling through its center is known as a hemi. It is a half-spherical curve combined with a planar circular area.

In real life, hemispheres can be found in the northern and southern halves of the Earth, A half-cut watermelon, the left and right parts of our brain, a bowl, and an igloo.

What is the Volume of Hemisphere?

In geometry, a hemisphere is a 3D solid object that is half the size of a sphere. The hemisphere is generated when a sphere is divided into two equal pieces in the middle. The volume of a hemisphere is the amount of things that can be held by a hemisphere. In other terms, the volume of a hemisphere is the number of unit cubes that can fit inside it. Because cubic units are the unit of volume, the volume of a hemisphere can be expressed as m3, cm3, in3, and so on.

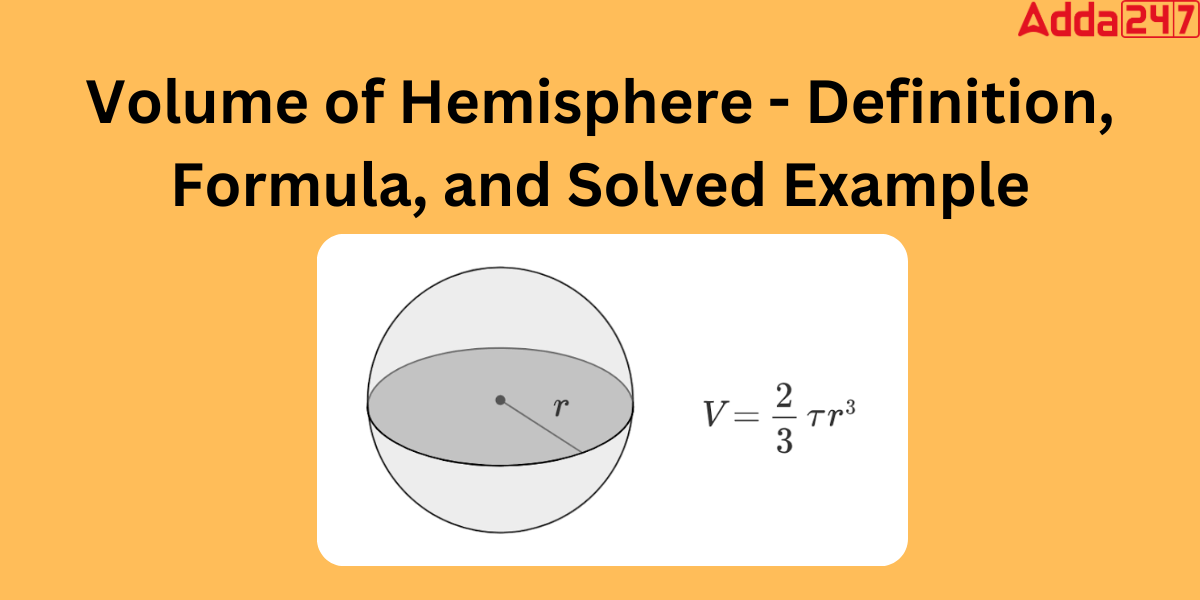
Volume of Hemisphere Formula

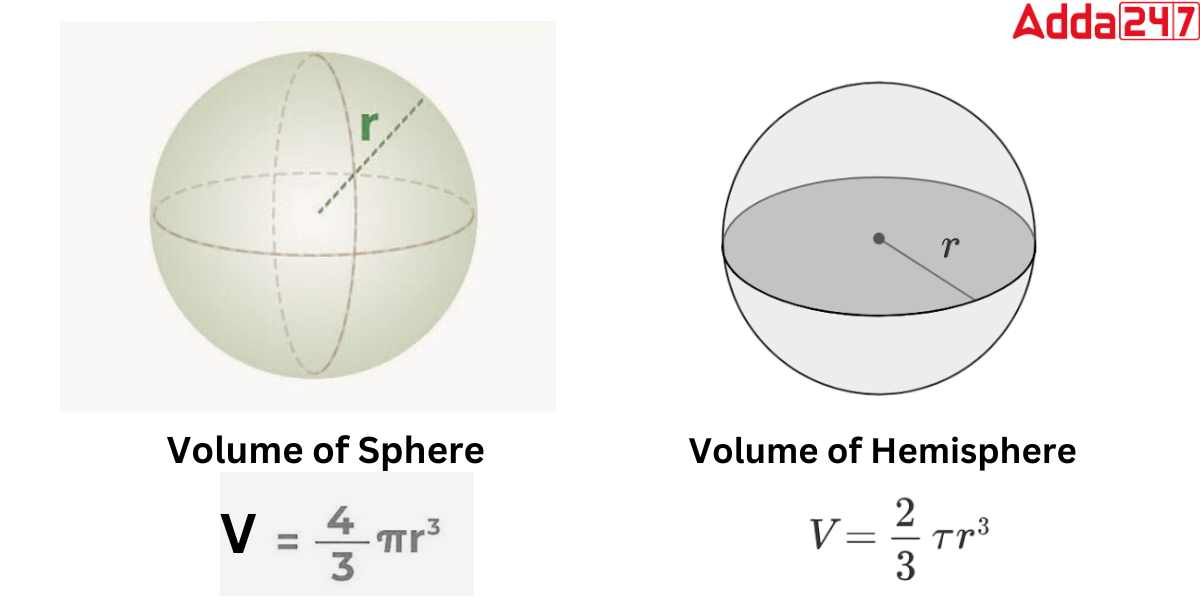
Archimedes derives the volume of a hemisphere. A hemisphere is a three-dimensional (three-dimensional) form that is half the size of a sphere. It features one flat circular base and one curved surface. Because the sphere’s base is circular, we can readily calculate its volume. The Volume of  hemisphere is equal to two-thirds multiplied by pi multiplied by radius to the power 3. As a result, the formula for calculating the volume-hemisphere is

Volume of Hemisphere= 2/3 πr³

Where is the “π” constant with an estimated value of 3.14 and “r” denotes the hemisphere’s circular radius.

How to Find Volume of a Hemisphere?

The formula Volume of hemisphere = 2πr³/3 is used to determine the volume of a hemisphere. So let’s calculate the volume of a hemisphere with a 9-unit radius. To calculate the volume of a hemisphere, follow the steps below.

Step 1: Take note of a hemisphere’s radius. Here, radius (r) equals Nine units.
Step 2: Replace the radius value in the equation Volume of hemisphere = 2πr³/3 and express the result in cubic units.
Step 3: Using r = 9 as a substitute, we obtain Volume of hemisphere = 2πr³/3 = (2 × 3.14 × 9³)/3 = 156.047 cubic units.

Hemisphere Equation

The equation for the hemisphere is given by when the radius “R” is centered at the origin.

x² + y² + z² = R²

A hemisphere with radius “R” at the location (x₀, y₀, z₀) has the following Cartesian form/equation:

(x-x₀)² + (y- y₀)² + (z- z₀)² = R²

As a result, the hemisphere’s spherical coordinates are as follows.

x = r cos θ sin ∅

y = r sin θ cos ∅

z = r cos ∅

Derivation of Volume of Hemisphere Formula

We can easily remember the volume of Hemisphere formula if we know its derivation. Let’s Take a look at the derivation of the volume of the Hemisphere formula

According to the definition of hemisphere, a hemisphere is a three-dimensional (3D) form that is half of a sphere. The shape formed when a sphere is cut by a plane traveling through its center is known as a hemisphere.

Since a hemisphere is half of a sphere, we may calculate the volume of a hemisphere by dividing the volume of a sphere by two.

Let us now assume that the radius of a sphere is r.

The formula can be used to calculate the volume of a sphere.

Sphere Volume = 4πr³/3

So, The Volume of hemisphere is = 1/2 of Sphere Volume

Or, Volume of hemisphere = 1/2 × 4πr³/3 = 2πr³/3 cubeunits.

Volume of Hemisphere Formula Solved Examples

Example 1: Determine the volume of a hemisphere with a radius of 7 cm.

Solution: We can easily find out the Volume of hemisphere with a radius of 6 cm using the  2/3 πr³formula

Given that the Radius (r) of the Volume of hemisphere = 6 cm
The volume of a hemisphere = (2/3)πr³ cubic units.
In the formula, change the value of r with the given data.
V = (2/3) × 3.14 × 7³ cm³

Or, V = (2/3) × 3.14 × 7³ cm³

V  = 718.01 cm³
Hence, the Volume of the given hemisphere is 718.01 cm³.

Example 2: A hemispherical bowl has a radius of 10 cm. Determine the bowl’s volume.
Solution: Given that the radius of the hemispherical bowl is 10 cm,

The volume of  hemisphere = (2/3)πr³ cubic units.
In the formula, change the value of r with the given data.
V = (2/3) × 3.14 × 10³ cm³

Or, V = (2/3) × 3.14 × 10³ cm³

V  = 6280 cm³
Hence, the Volume of the given hemisphere is 6280 cm³.

Example 3: Determine the volume of a hemisphere with a radius of 5 cm.

Solution: 

Given that the Radius (r) of the Volume of hemisphere = 5 cm
The volume of a hemisphere = (2/3)πr³ cubic units.
In the formula, change the value of r with the given data.
V = (2/3) × 3.14 × 5³ cm³

Or, V = (2/3) × 3.14 × 5³ cm³

V  = 261.66 cm³
Hence, the Volume of the given hemisphere is 261.66 cm³.

Sharing is caring!