Wave optics, also known as physical optics or wave theory of light, is a branch of optics that explores the behavior of light as a wave.

Name some phenomena that can be explained only through the wave nature of light.

Interference, Diffraction, and Polarization are some of the concepts that can be explained only when we consider light as a wave.

Give the difference between wave optics and geometrical optics.

A simplified representation of light that ignores the fact that light is a wave is known as geometrical optics. This model makes the assumption that light travels in straight lines and that it will either reflect or refractively interact with objects. In many cases, this model can be used to anticipate how light would behave; however, it becomes unreliable when things are very small or when light waves interact with one another. Wave optics studies phenomena that geometrical optics is unable to explain by taking into consideration the wave component of light.

Explain constructive and destructive interference.

The two waves will merge to create a momentarily larger wave with an amplitude equal to the sum of the amplitudes of the individual waves if their crests and troughs line up precisely. We refer to this as constructive interference. On the other hand, if the crests of two waves coincide with each other's troughs, they either combine to form a smaller wave or entirely cancel each other out. We refer to this as destructive interference.

Wave Optics Class 12 Notes, Formulas Sheet, List, PDF

Table of Contents

Wave Optics is an important concept in the realm of the study of light that explains some of the most fascinating phenomena of nature. The study of light and other electromagnetic waves and their interactions with matter is the focus of the field of wave optics. Wave optics considers the wave-like characteristics of light, in contrast to geometric optics, which views light as a collection of rays. This enables us to understand occurrences like polarization, diffraction, and interference. In this article, we will get to know about the different concepts of wave optics along with its formula and solved examples.

Wave Optics

The study of how light behaves when it travels in waves is known as wave optics. Images may be produced and objects can be illuminated using wave optics. Moreover, it can be applied to quantify material qualities and ascertain molecular structure. One area of physics that addresses the wave aspect of light is called wave optics. The foundation of it is the wave theory of light, initially put forth in 1678 by Dutch physicist Christiaan Huygens. The study of light propagation and its interactions with matter is accomplished through the application of wave optics. Wave Optics is also known as Physical Optics.

Wave Optics Meaning

Let us understand the meaning of wave optics by understanding its detailed background. Wave optics bears evidence to a well-known impasse between two eminent scientific societies that devoted their entire existence to comprehending the properties of light. One affirms that light is a particle, whereas the other affirms that light is a wave.

Known for his corpuscular theory, which postulates that “light consists of extremely light and tiny particles known as corpuscles which travel with very high speeds from the source of light to create a sensation of vision by reflecting on the retina of the eye,” Sir Isaac Newton is a well-known figure who supported the voice of the particle nature of light.

Newton was able to explain reflection and refraction using this theory, but he was unable to explain interference, diffraction, and polarization. Newton’s corpuscular hypothesis was mostly unsuccessful because it was unable to explain why light traveled at a slower speed in a denser medium than it did in the vacuum. This concept could be experimentally and theoretically proved by the wave optics. In this way, the wave optics came into being.

These theories aid in our comprehension of how light behaves in various contexts. They can be used to estimate the amount of light that will be dispersed or reflected, as well as to forecast how light will interact with its surroundings. These theories can often be extended to different kinds of waves, including water or sound waves.

Wave Optics Class 12

The phenomena of wave optics is given in a detailed manner in the wave optics chapter of class 12th. The wave optics concept is included in the form of a chapter in class 12th Physics NCERT book. The chapter features at chapter number 10. This chapter is highly important from the board examination point of view and has a high weightage in the board exam. Not only this, the chapter has a significant weightage in the physics section of the competitive exams. For the convenience of students, we have given below some of the most important topics from this chapter that is a must do for the board and competitive exam.

Theory of diffraction
Theory of interference
Young’s Double Slit Experiment
Huygens’ principle
Fresnel equations
Maxwell Electromagnetic Theory
Polarization

Wave Optics Class 12 Notes

Wave Optics is a must-do chapter when it comes to class 12th. This chapter explains many important phenomena of light ranging from polarization and diffraction. So, students must prepare this chapter by heart to get conceptual clarity and good marks in the exam. To aid students in their preparation journey, we have provided students with some important notes on this chapter.

The behavior of light when it comes into contact with an obstruction is explained by the theory of diffraction. Light waves scatter in all directions when they come into contact with an obstruction. The obstacle’s size and shape affect how much scattering occurs.
The behavior of light in the presence of two or more barriers is explained by the idea of interference. Light waves interact with one another as they come into contact with two or more obstacles, producing a pattern of bright and dark areas.
A reflecting surface can be used to illustrate how light behaves when it comes into contact with Huygens’ principle. Light waves are reflected in a direction perpendicular to the reflecting surface when they come into contact with it. It used the fact that light is a wave to explain reflection.
One can compute the amount of light reflected from a reflecting surface using the Fresnel equations. The formulas consider the thickness of the reflecting surface, the refractive index of the material, and the angle of incidence.
The behavior of light in all circumstances is explained by the Maxwell Electromagnetic Theory. The electric and magnetic fields related to light waves are considered in the theory.

Wave Optics Class 12 Notes PDF

Some of the important notes of the wave optics for class 12 students is given below for download in the PDF form.

Wave Optics Notes Class 12 PDF

Wavefront and Wave Normal

The location of every point in the medium vibrating at the same phase is known as a wavefront. Wavefronts can be classified into three categories based on the form of the light source. These three types of wave fronts are spherical wavefronts, cylindrical wavefronts and plane wavefronts. We can change the shape of wavefronts using a lens. The shapes of these wavefronts are illustrated below through a diagram.

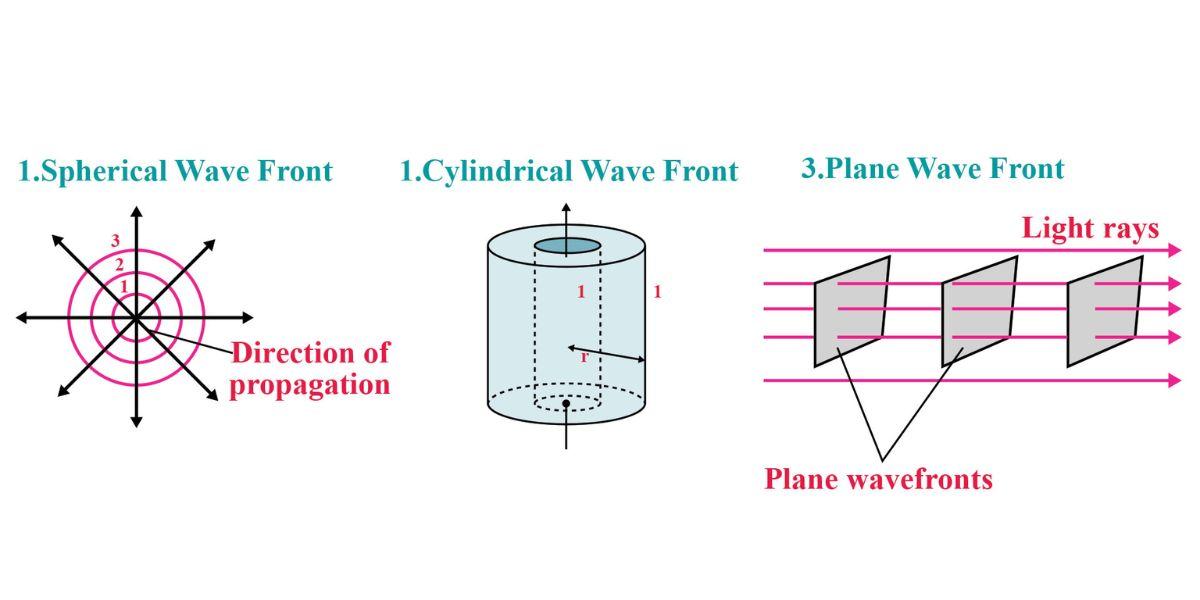
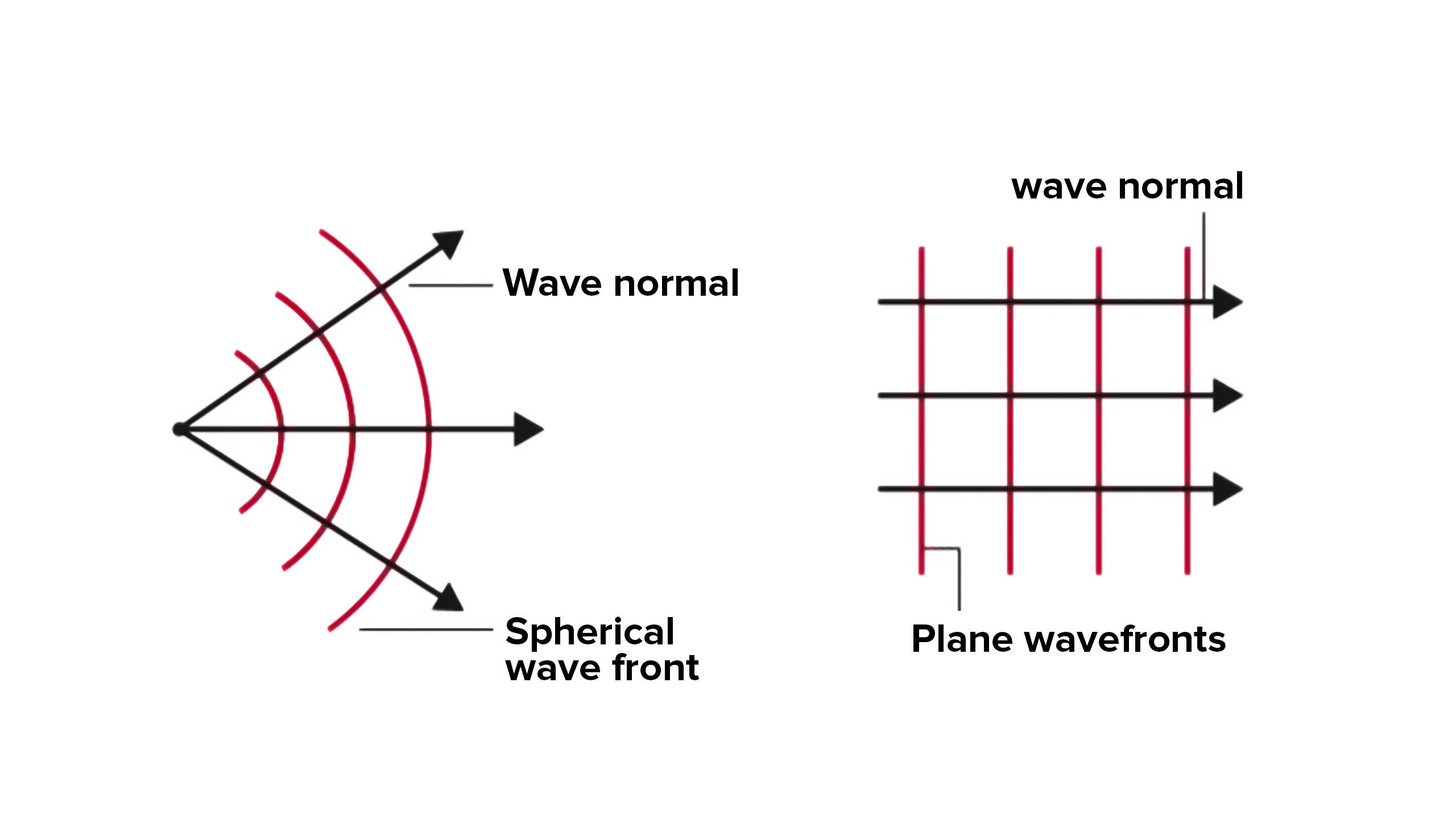
“Wave normal” refers to a perpendicular drawn to a wavefront’s surface at any point along the light’s path of propagation. A “ray” of light is the direction in which light travels. A light beam and a wave normal are thus the same thing. The same is depicted hereunder.

Huygen’s Principle

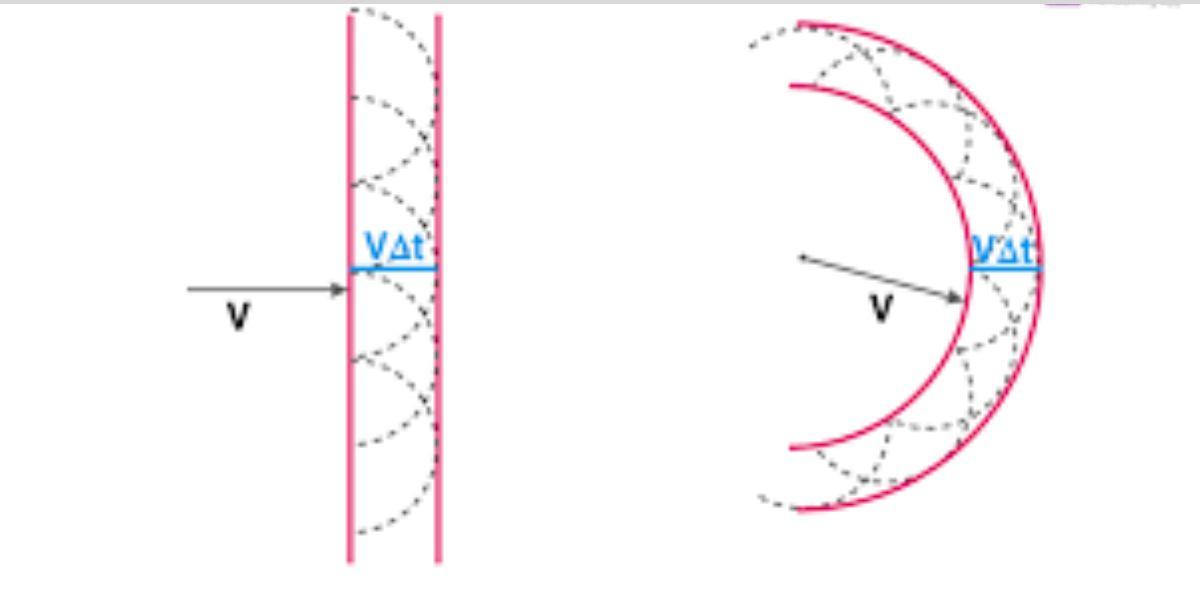
Huygen’s principle states that each point on a wavefront can be thought of as a separate source of disturbance that radiates secondary wavelets, which are spherical wavelets. The secondary wavelets propagate in every direction in tandem with the wave’s velocity.

The position and shape of the new wavefront at any given instant (Δt) can be determined by a surface that touches these secondary wavelets tangentially in the forward direction. We refer to this as the “secondary wavefront.”

Huygen’s theory of secondary wavelets, which was covered in the introduction, provides an explanation for a variety of optical phenomena, including diffraction, reflection, refraction, and interference. However, it was still unable to explain why wavefronts of secondary wavelets form forward rather than backward.

Maxwell Electromagnetic Theory

Maxwell argues that light is not a wave that moves mechanically. It is a transverse electromagnetic wave with a defined speed that is determined by,

C = 1/√μ0ε0 = 3 x 10⁸m/s

where, μ0 = permeability of the medium = 4π x 10^-7

ε0 = permissibility of the medium = 8.854 x 10^-12

Light Interference

Interference refers to the non-uniform energy distribution caused by two superimposed light waves in a material. To understand the concept of light interference, one must need to have a proper knowledge of the coherent and incoherent sources of light.

Coherent Source: Coherent sources are two sources that continuously generate monochromatic light with a phase difference of 0 or constant.

Incoherent Source: Incoherent sources are those that do not continuously vary in phase when they emit light.

Wave Optics Formulas Sheet and List

The wave optics formula is important for students for the revision purpose as well as for the competitive exams as well. To help students, we have provided some of the important formulas for wave optics below.

Details		Formula
The path difference of two coherent Waves		∆d=d2–d1 ∆d is the path difference
The Path difference of two coherent waves: Interference Maximum		∆d=k.λ ∆d is path difference λ is the wavelength
The path difference of two coherent waves: Interference Minimum		∆d=((2.k+1).λ)/2∆d is path difference λ is the wave length
Thin-film interference: Constructive (maximum)		2ntcosr=(n+1/2)λt is film thickness n is refractive index r is refraction angle λ is wave length
Thin-Film interference: destructive (minimum)		$2 n t cosr = nλ$ t is film thickness n is refractive index r is refraction angle λ is wave length
Radii of Newton’s Ring		r=√(k.R.λ) or $r = \sqrt (((2. k + 1) . R . λ)) /2$ r is the radius R is the radius of curvature λ is the wavelength
Light Diffraction		$I = d² / (4. λ)$ I is the distance from obstacle d is the obstacle size λ is wavelength
Diffraction grating: maximum (bright stripes)		$d s in θ = kλ$ d is the lattice constant is the diffraction angle λ is the wavelength
Diffraction grating (dark stripes)		dsinθ=(K+1/2)λd is the lattice constant is the diffraction angle λ is the wavelength

Wave Optics Formula Based Examples

Some of the solved examples on the topic of wave optics is given hereunder. These solved examples will help students apply the learn formulas in a better way.

Example 1: Given the wavefront to be spherical, what will be the amplitude of the wave at a distance of 4 units if the amplitude of the spherical wavefront at a distance of 2 units from the source is 10 units.

Solution: As we know, the relation between the amplitude A and distance r from the center is given by:

A ∝ 1/r²

so, A1/A2 = r2²/r1² ——-(1)

given, A1 = 10 units

r1 = 2 units

r2 = 4 units

substituting these values in equation (1), we get

10/A2 = 4²/2²

10/A2 = 16/4

A2 = 10/4

A2 = 2.5 units

Example 2: Young’s double-slit experiment uses a beam of light with two wavelengths—650 nm and 520 nm—to produce interference fringes. Determine the separation between the third brilliant fringe on the screen and the 650 nm wavelength central maxima.

Solution: Given,

beam’s wavelength of light (λ1) = 650 nm

The other light beam’s wavelength (λ2)= 520 nm

Let the slits’ separation from the screen = D

Let the two slits’ distance from one another = d

The relation that provides the distance between the central maxima and the nth bright fringe on the screen is given as

x = n x λ1 (D/d)

given n = 3

so, x = 3 x 650 x (D/d)

Hence, x = 1950 (D/d) nm

Example 3: The red shift of the hydrogen emission in a star, measured at 6563 Å Hα, is determined to be 15 Å. Calculate how quickly the star is moving away from Earth.

Solution: Given,

λ = 6563 Å

Δλ = 15 Å

The velocity (v) will be negative since the star is moving away.

So, Δλ = – vλ/c

as, v is equal to –cΔλ/λ.

= -(3 x 108) x (15 Å/6563 Å) =

Hence, λ= 6.86 x 10⁵ m/s