Quadrilateral
Quadrilateral Meaning in Math: The Latin words quadra, which means four, and latus, which means sides, are combined to form the English word quadrilateral. In geometry, A polygon with four sides, four angles, and four vertices is referred to as a quadrilateral. A closed shape known as a quadrilateral is formed by connecting four points, any three of which cannot be collinear. In this article, we are going to learn more about Quadrilateral, its Properties, classification, and formulas.
What is Quadrilateral
A polygon with four sides, four angles, and four vertices is called a quadrilateral. As suggested by the name, it always has four sides, four angles, and four vertices. The quadrilateral has angles at each of its four vertices, or corners. The sum of 4 angles is always 360 degrees. In the below figure.ABCD is a quadrilateral.
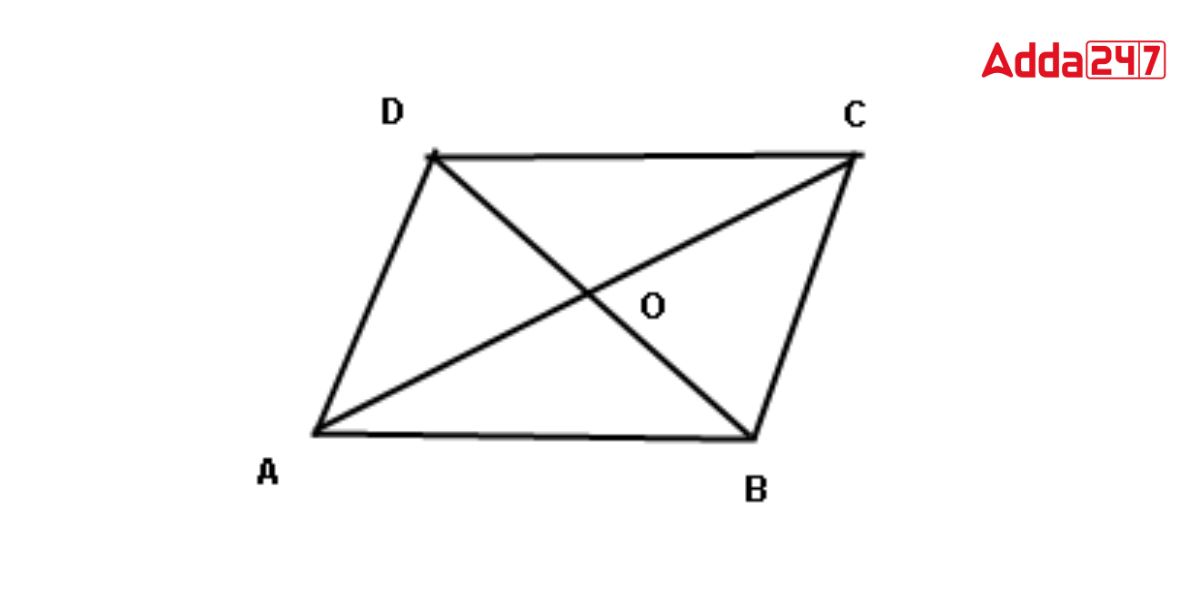
In the above ABCD Quadrilateral,
- The quadrilateral ABCD’s four angles are ∠A, ∠B, ∠C, and ∠D
- The four sides of the quadrilateral ABCD are AB, BC, CD, and DA.
- The quadrilateral ABCD’s four vertices are A, B, C, and D.
- The quadrilateral ABCD’s two diagonals are AC and BD.
Quadrilaterals Meaning
A quadrilateral is a polygon with four sides and four angles. It is a fundamental shape in geometry and is characterized by its straight sides and four corners or vertices. Quadrilaterals come in various types and have distinct properties based on their side lengths, angles, and other geometric characteristics.
Here are some common types of quadrilaterals:
- Rectangle:
- A rectangle has four right angles (90-degree angles).
- Opposite sides are equal in length and parallel.
- Diagonals are congruent and bisect each other.
- Square:
- A square is a special type of rectangle where all sides are equal in length.
- All angles are right angles (90 degrees).
- Diagonals are congruent and bisect each other.
- Parallelogram:
- Opposite sides are equal in length and parallel.
- Opposite angles are equal in measure.
- Diagonals bisect each other.
- Rhombus:
- A rhombus is a special type of parallelogram where all sides are equal in length.
- Opposite angles are equal in measure.
- Diagonals are perpendicular and bisect each other.
- Trapezoid (Trapezium in British English):
- A trapezoid has exactly one pair of parallel sides.
- The non-parallel sides are called legs.
- The angles can vary in measure.
- Kite:
- A kite is a quadrilateral with two pairs of adjacent sides that are equal in length.
- One diagonal is a perpendicular bisector of the other.
- Isosceles Trapezoid:
- A trapezoid where the legs are equal in length.
- The base angles are equal in measure.
- Cyclic Quadrilateral:
- A quadrilateral that can be inscribed in a circle.
- The opposite angles are supplementary (sum to 180 degrees).
These are just a few examples of the many types of quadrilaterals. Each type has its own unique properties, angles, and relationships between sides and diagonals. Quadrilaterals are studied extensively in geometry and have applications in various fields, including architecture, engineering, and design.
Quadrilateral Examples
A quadrilateral is a two-dimensional shape that has four sides, four angles, and four vertices. A quadrilateral does not always have to have equal lengths on each of its four sides. As a result, depending on the sides and angles, we have several types of quadrilaterals. There are four different types of quadrilaterals: There are many different types of quadrilateral examples, such as
- Trapezium
- Parallelogram
- Squares
- Rectangle
- Rhombus
- Kite
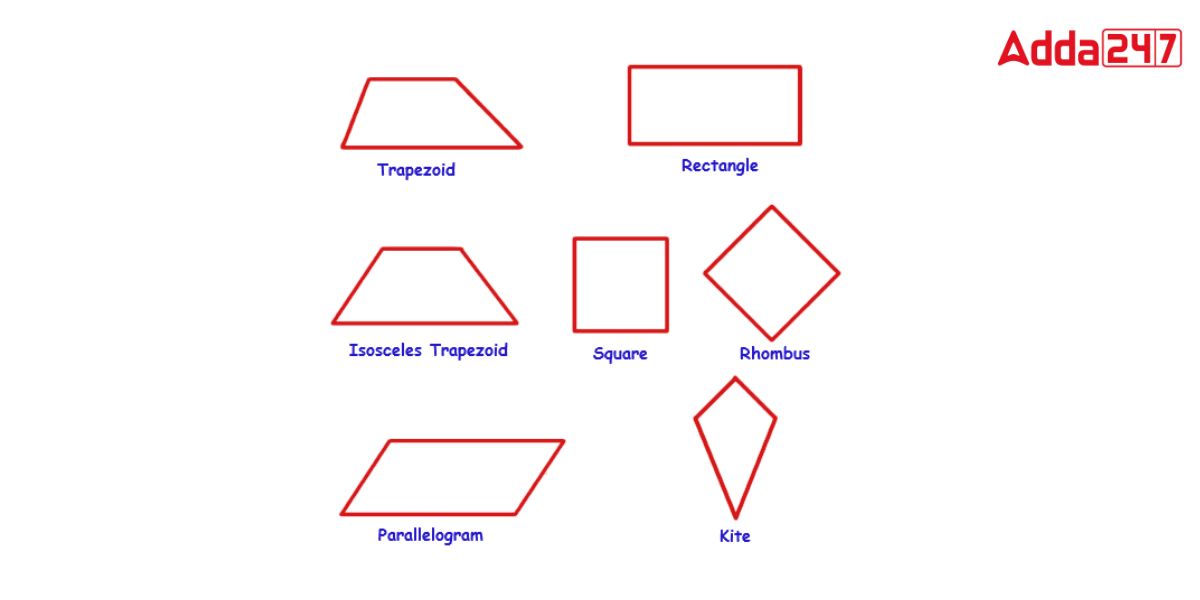
Quadrilateral Properties
The following quadrilaterals each have unique characteristics. Nevertheless, all quadrilaterals have a few characteristics. They are listed below.
- Quadrilaterals have four sides.
- They have four vertices.
- There are two diagonals in each
- They have four interior angles.
- The Sum of all interior angles of a quadrilateral is 360°
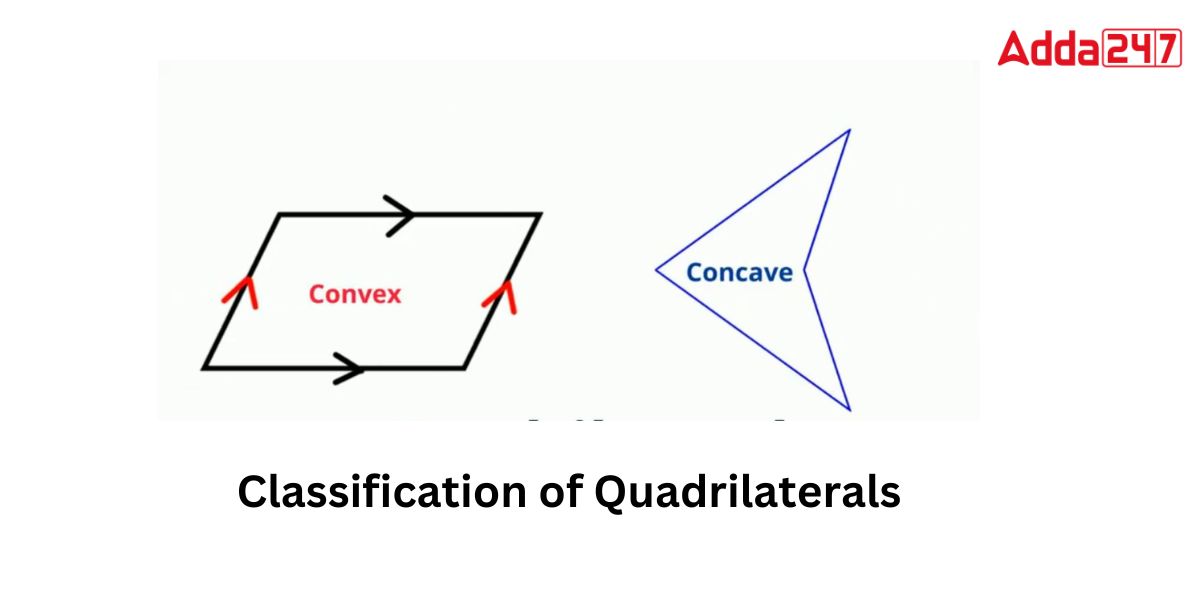
Classification of Quadrilaterals
The basic classification of the quadrilaterals is between convex and concave quadrilaterals. Types of quadrilaterals are separated into different groups based on their properties. These quadrilaterals that are concave and convex can be divided further into their subgroups.
Concave Quadrilaterals: Concave quadrilaterals are polygons with four sides and an interior angle larger than 180. A convex quadrilateral’s two diagonals are included in the enclosed figure.A Dart is an example of a concave quadrilateral.
Convex Quadrilaterals: A four-sided polygon with inner angles that are less than 180 degrees each is referred to as a convex quadrilateral. Squares, rectangles, parallelograms, rhombuses, kites, and trapezoids are examples of convex quadrilaterals (trapezium).
Types of Quadrilaterals and its Properties
Let’s take a look at the various types of quadrilateral and their properties with the figure.
Parallelogram
A quadrilateral with two sets of parallel sides is known as a parallelogram. In a parallelogram, the opposing sides are of equal length, and the opposing angles are of equal size.
Properties of Parallelogram:
- The opposing sides are equal and parallel.
- Angles on either side are equal.
- The adjacent or adjacent angles are supplementary.
- The two diagonals of the parallelogram are split in two.
- The parallelogram is divided into two congruent triangles by each diagonal.
- A parallelogram’s total square sum and the total square sum of its diagonals are equivalent. Also known as the parallelogram law.
Rhombus
A rhombus is a quadrilateral with opposite sides that are parallel to one another and equal opposite angles. A rhombus has equal lengths on all sides, making it an equilateral quadrilateral.
Properties of Rhombus:
- A rhombus has an equal number of sides.
- Every Rhombus has two diagonals that join the opposite vertices in pairs.
- A rhombus’ diagonals will always cut each other at a 90-degree angle.
- A rhombus is divided into four right-angled congruent triangles by its two diagonals.
- Any two parallel or following angles added together equal 180 degrees.
Trapezium
The trapezium is a quadrilateral in two dimensions with a single pair of parallel opposite sides. The bases and legs of a trapezium are its parallel and non-parallel sides, respectively.
Properties of Trapezium
- A trapezium has four sides, four vertices, and four angles.
- In A trapezium two parallel sides are known as bases and the other two non-parallel sides are called legs.
- Trapezium has one set of opposite sides which is parallel to the other.
- In a trapezium, the sum of all four internal angles is always 360°.
Rectangle
A quadrilateral with equal angles and parallel opposite sides is known as a rectangle.Each rectangle shape has two dimensions: length and width. All of a rectangle’s angles are equal to 90 degrees, and its opposite sides are equal and parallel to one another.
Properties of Rectangle:
- Each of a rectangle’s opposing sides is equal and parallel to the other.
- At each vertex, a rectangle’s inner angle is 90°.
- The sum of all interior angles is 360°.
- Each of the diagonals is divided in half.
- The diagonals are equal in Length
Square
A quadrilateral with four equal sides is called a square. Equal sides and internal angles that are both 90 degrees distinguish each square shape.
Properties of Square:
- A Square has four sides and four vertices.
- The square’s four sides are equal to one another.
- Each vertex of a square has a 90° internal angle.
- The Sum of all interior angles is 360°.
- A square’s diagonals are parallel to one another.
- The diagonals are all the same length.
Kite
A kite is a quadrilateral that has two sets of adjacent, equal-length sides. A kite has four vertices, four sides, and four angles.
Properties of Kite
- A kite has two adjacent pairs of equal sides.
- It has a single pair of equal, obtuse, opposite angles.
- In the intersection of the two angles, the two sides are equally sized.
- It has two diagonals that right-angle intersect with one another.
- The diagonals are parallel with one another.
- The longer diagonal splits the two opposing angles in half.
- A kite has symmetry along its main diagonal.
Quadrilateral Formula
There are two fundamental quadrilateral formulas, which are as follows:
- Area of Quadrilateral
- Area of Quadrilateral
Area of Quadrilateral
The area of the Quadrilateral refers to the total amount of space that is enclosed by a quadrilateral. Below is a list of the different types of quadrilaterals area formulas:
| Types of Quadrilateral | Area Formula |
| Parallelogram | Base x Height |
| Rectangle | Length x Width |
| Square | Side x Side |
| Rhombus | (1/2) x Diagonal 1 x Diagonal 2 |
| Trapezium | ½ (Sum of parallel sides)(Distance between parallel sides) |
| Kite | 1/2 x Diagonal 1 x Diagonal 2 |
Perimeter of Quadrilateral
In order to determine the path that encircles a quadrilateral, we must add the lengths and widths of each of its four sides, with lengths being the longest and widths being the shortest. Perimeter is calculated using the formula Perimeter = Length + Length + Width + Width.
Here is a list of Perimeter formulas for different types of quadrilaterals
| Types of Quadrilateral | Formula of Perimeter |
| Square | 4 x Side |
| Rectangle | 2(Length + Breadth) |
| Parallelogram | 2(Base + Side) |
| Rhombus | 4 x Side |
| Trapezium | Sum of all four sides |
| Kite | 2 (a + b), a and b are adjacent pairs |
Quadrilateral Definition, Meaning, Properties, Examples QNAs
Q.What is a Quadrilateral?
A polygon with four sides, four angles, and four vertices is called a quadrilateral. As suggested by the name, it always has four sides, four angles, and four vertices.
Q.Why are they called quadrilaterals?
A polygon with four sides, four angles, and four vertices is called a quadrilateral. The Latin words Quadri, which means four, and latus, which means side, were combined to create the English word quadrilateral.
Q.Who invented quadrilateral?
The first mathematician to present the formula for the area of a cyclic quadrilateral was Brahmagupta (ad 628) His explanation of how to locate a cyclic quadrilateral with rational sides is the first of its kind.
Q.What are 3 facts about quadrilaterals?
The following quadrilaterals each have unique characteristics. Three Facts about quadrilaterals are
- Quadrilaterals have four sides.
- They have four vertices.
- There are two diagonals in each









 NEET UG 2026 Registration: NTA releases ...
NEET UG 2026 Registration: NTA releases ...
 CUET UG 2026 Online Registration Started...
CUET UG 2026 Online Registration Started...
 CUET 2026 Free Batches Launched by CUET ...
CUET 2026 Free Batches Launched by CUET ...














